Les facteurs de coût associés aux dépenses en médicaments d'ordonnance – Un rapport méthodologique

ISBN : 978-0-660-21541-9
No cat. : H82-15/2013F-PDF
Décembre 2013
La version PDF
Résumé
Les dépenses en médicaments d'ordonnance représentent une partie significative des coûts des soins de santé au Canada; on estime que les dépenses ont atteint 27,7 milliards de dollars en 2012. Après plusieurs années de croissance à deux chiffres, les taux de variation de ces dépenses ont graduellement diminué ces dernières années et on prévoit qu'elles atteindront en 2012 leur plus bas niveau en 16 ans1.
Les variations des dépenses en médicaments d'ordonnance sont imputables à de nombreux facteurs. Par exemple, bien que la récente baisse du taux s'explique principalement par le lancement de produits génériques et par les réformes du prix des médicaments génériques, on s'attend à ce que les nouvelles thérapies coûteuses, de même que les hausses du volume de médicaments utilisés continuent de stimuler la pression à la hausse sur les coûts.
Compte tenu de la complexité des forces à l'œuvre, les simples statistiques sur l'utilisation et les coûts des médicaments ne donnent qu'un aperçu limité des facteurs qui stimulent la croissance. La détermination des principaux facteurs et la compréhension de l'effet qu'ils ont sur les dépenses en médicaments d'ordonnance permettent aux décideurs et aux chercheurs de prévoir les pressions sur les coûts et les niveaux de dépenses à venir.
Le présent rapport méthodologique (i) décrit les facteurs de coût associés aux dépenses en médicaments d'ordonnance, (ii) discute des exigences en matière de données et des approches appliquées à l'analyse et (iii) fournit la méthodologie et les formules qui permettent de décomposer la variation liée aux dépenses en médicaments d'ordonnance et d'évaluer ses facteurs.
L'approche en trois niveaux fournit (i) aux décideurs de haut niveau une excellente compréhension des facteurs attribuables aux dépenses en médicaments, (ii) aux chercheurs qui souhaitent comprendre les analyses des facteurs de coût une description des mécanismes de base de cette méthode et (iii) aux chercheurs qui planifient la réalisation de véritables analyses des facteurs de coût en s'appuyant sur une méthodologie intégrale et les formules qui en découlent.
Les facteurs de coût associés aux dépenses en médicaments d'ordonnance
Le présent rapport examine les facteurs associés aux deux composantes des dépenses en médicaments d'ordonnance : les coûts des médicaments et les frais d'exécution des ordonnances.
Facteurs associés aux coûts des médicaments
Les facteurs associés aux coûts des médicaments sont regroupés en quatre grandes catégories d'effets. Chaque effet illustre l'incidence du changement sur le facteur qui y correspond :
- Effets « prix »
- Effet « variation de prix » – variations du prix des produits de marque et des produits génériques
- Effet « substitution par un médicament générique » – passage des produits de marque aux produits génériques
- Effets « volume »
- Effet « volume des ordonnances » – variations du nombre d'ordonnances administrées aux patients
- Effet « nombre d'ordonnances » – variations du nombre moyen d'unités par ordonnance
- Effet « dosage-forme galénique des médicaments » – variations de l'utilisation du dosage ou des formulations d'une molécule
- Effets « combinaison de médicaments »
- Effet « médicament existant » – variations de l'utilisation de médicaments disponibles pendant les deux périodes analysées
- Effet « médicament retiré du formulaire » – variations de l'utilisation de médicaments qui ont été retirés du formulaire à la deuxième période
- Effet « nouveau médicament » – variations pour passer de l'utilisation de médicaments existants à celle de médicaments qui ont fait leur apparition sur le marché au cours de la deuxième période
- Effets « démographiques »
- Effet « population » – variations du nombre de consommateurs de médicaments
- Effet « vieillissement » – variations de la distribution de la population selon les tranches d'âge
- Effet « sexe » – variations de la distribution de la population en fonction du sexe
Bien que ces effets expliquent les variations des prix des médicaments, ils peuvent être influencés par des facteurs qui sont difficiles à évaluer. Ceux-ci comprennent la prévalence des maladies, les pratiques en matière de prescription et les facteurs socioéconomiques.
Facteurs associés aux frais d'exécution d'ordonnances
De plus, le rapport cerne trois facteurs associés aux frais d'exécution d'ordonnances.
- Effet « frais d'exécution des ordonnances » – Variations des frais d'exécution d'ordonnances
- Effet « nombre d'ordonnances » – Variations du nombre moyen d'unités par ordonnance
- Effet « volume des médicaments » – Variations du nombre d'unités administrées
Les effets « démographiques » énumérés ci-dessus peuvent aussi être calculés en fonction de la partie liée aux frais d'exécution des ordonnances des dépenses en médicaments d'ordonnance.
Approche de base
La méthodologie proposée dans le présent rapport applique l'approche de Laspeyres pour décomposer le coût en deux déterminants ou facteurs : le prix et la quantité. En comparant deux périodes de temps, cette approche isole l'effet de la variation d'un facteur précis (p. ex. le prix) en maintenant l'autre facteur (p. ex. la quantité) constant à sa valeur pendant la période de référence.
Les nombreux facteurs de coût associés aux dépenses en médicaments d'ordonnance peuvent être isolés et quantifiés si l'on étend l'approche de Laspeyres à un cadre multifactoriel.
Exigences en matière de données
Pour ce type de cadres, en plus du prix de base et des renseignements sur la quantité, il est nécessaire d'avoir des renseignements sur les médicaments pour chacune des deux périodes de temps comparées (p. ex. le nom de la molécule, le dosage, la forme, le type de médicament, qu'il soit de marque ou générique, etc.) Si l'on dispose de renseignements démographiques, il est possible de les intégrer à la méthodologie.
Ces données peuvent être disponibles dans des bases de données administratives et présenter de l'information sur les médicaments expédiés, vendus, administrés ou remboursés au Canada. Cela comprend des données sur les régimes publics et privés d'assurance-médicaments, des données sur les ventes de médicaments dans les pharmacies, des données sur les expéditions de médicaments, des données provenant des hôpitaux, etc. Ces ensembles de données peuvent être utilisés pour déterminer les facteurs de coût associés aux dépenses en médicaments d'ordonnance en fonction de la méthodologie proposée.
Formules
Le rapport présente une section technique détaillée qui comporte une discussion de la méthodologie et des démonstrations étape par étape expliquant comment les formules ont été calculées. Pour chacun des effets, une formule mathématique est présentée.
Étant donné qu'il peut y avoir plus d'une façon de mener une analyse des facteurs de coût selon l'objectif et la précision analytique de la recherche et la disponibilité des données, le rapport porte également sur l'examen de la façon dont la méthodologie proposée peut être ajustée et améliorée.
Des discussions détaillées concernant la méthodologie et les formules des effets croisés résiduels sont fournies en annexe.
Remerciements
Le présent rapport a été rédigé par le Conseil d'examen du prix des médicaments brevetés (CEPMB) au titre du Système national d'information sur l'utilisation des médicaments prescrits (SNIUMP).
Le CEPMB tient à remercier les personnes suivantes pour leurs contributions :
- Les membres du Comité directeur du SNIUMP pour leur supervision spécialisée et leur orientation dans le cadre de la rédaction du présent rapport.
- L'Institut canadien d'information sur la santé, pour avoir passé en revue et commenté sur la méthodologie proposée dans le présent rapport.
- M. Steve Morgan, Ph. D., pour avoir révisé la méthodologie proposée dans le présent rapport et prodigué ses conseils en qualité de spécialiste en cette matière.
- Les membres du personnel du SNIUMP du CEPMB pour leur contribution au contenu analytique du rapport, notamment Mme Elena Lungu, gestionnaire intérimaire du SNIUMP, M. Orlando Manti, gestionnaire en économie, ainsi que le groupe scientifique et l'équipe éditoriale du CEPMB.
Avis de non-responsabilité
Le SNIUMP est une initiative de recherche qui fonctionne indépendamment des activités de réglementation du Conseil. Les déclarations et les opinions exprimées dans le présent rapport du SNIUMP ne représentent pas la position officielle du CEPMB.
1 ICIS. Dépenses en médicaments au Canada, de 1985 à 2012. Ottawa, Institut canadien d'information sur la santé, 2013. Sur Internet : https://secure.cihi.ca/free_products/Drug_Expenditure_2013_FR.pdf.
1. Introduction
Les dépenses en médicaments d'ordonnance représentent une partie significative des coûts des soins de santé au Canada : on estime qu'environ 27,7 milliards de dollars ont été dépensés pour des médicaments d'ordonnance en 2012. Après plusieurs années de croissance à deux chiffres, les taux de variation de ces dépenses ont graduellement diminué ces dernières années et on prévoit qu'elles atteindront en 2012 leur plus bas niveau en 16 ans (ICIS, 2013).
Facteurs – Le niveau des dépenses en médicaments d'ordonnance est déterminé par de nombreux facteurs ou déterminants, comme la taille et l'âge de la population, le volume et le type de médicaments utilisés, les niveaux de prix, etc.
Facteurs de coût – Une variation de l'un de ces facteurs constitue un facteur de coût. Par exemple, on s'attend à ce que les variations des parts de marché de produits de marque par rapport à celles des produits génériques engendrent une baisse du taux de croissance des dépenses en médicaments d'ordonnance en raison du lancement de produits génériques. D'autre part, on s'attend à ce que les nouvelles thérapies coûteuses stimulent la pression à la hausse sur les coûts.
Effets – Intuitivement, on s'attend à ce que ces facteurs de coût entraînent des variations du niveau des dépenses en médicaments d'ordonnance. La mesure de l'incidence précise d'un facteur sur ces éléments s'effectue en déterminant son effet. Si l'on compare deux périodes de temps, l'effet sur les dépenses peut être calculé si l'on permet la variation d’un facteur tout en maintenant les autres facteurs à leurs valeurs pendant la période de référence.
Compte tenu de la complexité des forces à l'œuvre, les simples statistiques sur l'utilisation et les coûts des médicaments ne donnent qu'un aperçu limité des facteurs qui stimulent la croissance. La détermination des principaux facteurs et la compréhension de l'effet qu’ils ont sur les dépenses en médicaments d'ordonnance permettent aux décideurs et aux chercheurs de prévoir les pressions sur les coûts et les niveaux de dépense de l'avenir. Différentes études ont précédemment été publiées concernant les facteurs qui contribuent à l'augmentation des coûts des soins de santé (CBO, 2008; ICIS, 2011) et, plus particulièrement, à l'augmentation du coût des médicaments (Morgan, 2002, 2004, 2005; Gerdtham et Ludin, 2004; ICIS, 2012).
Le présent rapport méthodologique s'appuie sur les travaux publiés précédemment, y compris ceux du CEPMB (CEPMB, 2004, 2006, 2011), et l'approche qu'on y propose a été élaborée en consultation avec l'Institut canadien d'information sur la santé (ICIS).
Le présent rapport fournit les outils nécessaires à l'analyse complète des facteurs associés aux dépenses en médicaments d'ordonnance en :
- décrivant les facteurs et l’effet qu'ils ont sur les dépenses en médicaments d'ordonnance (section 2);
- examinant les exigences en matière de données et les approches appliquées à l'analyse (section 3);
- fournissant la méthodologie et les formules permettant de décomposer les dépenses en médicaments d'ordonnance et de mener les analyses des facteurs de coût (section 4).
Dans le cadre du présent rapport, les facteurs associés aux deux composantes principales des dépenses en médicaments d'ordonnance – les coûts en médicaments et les frais d'exécution des ordonnances – sont analysés dans le contexte de quatre grandes catégories : les effets « prix », les effets « volume », les effets « combinaison de médicaments » et les effets « démographiques ». Chacune de ces catégories est de nouveau divisée en fonction d'effets plus spécifiques. Le présent rapport fournit des formules pour tous les effets pris isolément, ainsi que pour les effets croisés résiduels.
La méthodologie ne se limite pas aux analyses de tendances des variations en matière de ventes ou de dépenses en fonction du temps, elle peut aussi être utilisée dans la réalisation d'analyses entre les différentes administrations ou de comparaisons internationales visant à décomposer les sources d'écart entre les ventes ou les dépenses en médicament. De plus, si l'on utilise la méthodologie normalisée, il est possible de mener des analyses spécialisées de catégories thérapeutiques ou de segments de marché en particulier.
La méthodologie proposée peut être utilisée avec une grande variété de bases de données administratives, y compris les données sur les régimes publics et privés d’assurance-médicaments, les données sur les ventes de médicaments dans les pharmacies, les données sur les expéditions de médicaments et les données provenant des hôpitaux. Elle peut être ajustée et améliorée en fonction de la disponibilité des données ou alors de l'objectif et de la précision analytique d’une étude de recherche donnée (section 5).
Selon la source des renseignements, il est possible que les données disponibles ne tiennent pas explicitement compte de tous les facteurs, y compris la prévalence des maladies, les pratiques de prescription et les facteurs socioéconomiques. Par exemple, l'analyse des facteurs de coût permet de déterminer dans quelle mesure une variation des dépenses s'explique par une augmentation de l'utilisation, mais elle ne permet pas de quantifier la part de la hausse de l'utilisation qui est attribuable aux activités de commercialisation. La méthodologie proposée comporte un certain nombre de limites, qui sont décrites dans le présent rapport (section 6).
Des discussions en profondeur au sujet de la méthodologie et des formules sont présentées en annexe.
2. Aperçu des facteurs de coût associés aux dépenses en médicaments d’ordonnance
Les dépenses en médicaments d'ordonnance comprennent généralement deux composantes distinctes : le coût des médicaments et les frais d'exécution des ordonnances. Le coût des médicaments est le coût réel d'un médicament et peut comprendre les frais supplémentaires et les marges bénéficiaires des pharmacies. Les frais d'exécution des ordonnances sont les frais associés à un service facturé par le pharmacien au moment où celui-ci émet une ordonnance.
Bien qu'il s'agisse de deux types distincts de dépenses (le prix du médicament par rapport aux frais imputés pour les services), leur augmentation pourrait s'expliquer par un certain nombre de facteurs communs, comme l'évolution de la taille de la population, du vieillissement de la population et du volume des ordonnances.
Habituellement, les analyses des éléments de coûts mettent l'accent sur le coût réel des médicaments, qui représentent généralement la plus importante composante des dépenses en médicaments d'ordonnance (Morgan, 2002, 2004, 2005; Gerdtham et Ludin, 2004; CEPMB, 2004, 2006). Néanmoins, les modèles des facteurs de coût sont également appliqués aux frais d'exécution des ordonnances (CEPMB, 2011), puisqu'ils représentent une partie significative des coûts.
La présente section fournit un aperçu des effets qui peuvent être dégagés au moyen de la méthodologie proposée. Chaque effet illustre l'incidence d’un facteur précis sur le niveau de dépenses en médicaments d'ordonnance.
La section 2.1 examine les facteurs associés aux coûts des médicaments, la section 2.2 examine les facteurs associés aux frais d'exécution des ordonnances et la section 2.3 examine les facteurs associés à la partie des coûts versée par le régime d'assurance-médicaments. Les effets croisés sont abordés à la section 2.4.
Précisons que l'analyse des facteurs de coût ne se limite pas aux effets examinés et ne couvre pas nécessairement l'ensemble de ces effets. La section sur les ajustements et les améliorations apportées à la méthodologie (section 5) décrit la façon dont il faudrait adapter l'approche en fonction de la disponibilité des données et des besoins précis liés à la recherche.
2.1 Facteurs associés aux coûts des médicaments
Les facteurs associés aux coûts des médicaments peuvent être regroupés en quatre grandes catégories : les effets « prix », les effets « volume », les effets « combinaison de médicaments » et les effets « démographiques ». Chaque effet illustre l'incidence de la variation d'un facteur précis. Voici une description des effets pris isolément :
Effets « prix »
1. Effet « variation de prix »
Cet effet illustre l'incidence des variations du prix des médicaments et est déterminé en fonction du dosage, de la forme galénique et de l'indication de marque ou générique. Par exemple, les récentes réformes du prix générique qui ont entraîné une diminution des prix génériques ont un effet négatif sur la variation de prix du coût des médicaments.
2. Effet « substitution par un médicament générique »
Cet effet illustre l'incidence de la variation de l'utilisation pour passer des produits de marque plus coûteux aux produits génériques moins coûteux. On s'attend à ce que cet effet ait des valeurs négatives lorsque les produits génériques seront lancés.
Effets « volume »
3. Effet « volume des ordonnances »
Cet effet illustre l'incidence des variations du nombre d'ordonnances administrées à une population de patients normalisée au cours des deux périodes analysées. De nombreux facteurs peuvent avoir une incidence sur cet effet, y compris l'utilisation de nombreux médicaments, la présence de comorbidité, la persistance des traitements et des pratiques de prescription. De plus, en l'absence de données démographiques, l'effet « volume des ordonnances » illustre aussi le vieillissement de la population et les variations de la répartition selon le sexe, de même que les variations de la taille de la population qui utilise des médicaments.
4. Effet « nombre d'ordonnances »
Cet effet illustre l'incidence des variations du nombre moyen d'unités d'un médicament administrées par ordonnance. Une hausse de cette mesure contribue positivement à l'augmentation du prix des médicaments, à moins qu'elle ne soit compensée par une réduction du nombre d'ordonnances (p. ex. effet « volume des ordonnances »).
5. Effet « dosage et forme galénique »
Cet effet illustre l'incidence des variations de l'utilisation en fonction du changement du dosage ou des formulations d'une molécule (ingrédient actif). Les médicaments sont généralement offerts dans une variété de combinaisons de dosages et de formes galéniques pour lesquelles le coût par unité peut varier considérablement. Une hausse de l'utilisation des médicaments à dosage plus élevé peut contribuer de façon positive à la hausse des coûts des médicaments, puisque les médicaments à dosage plus élevé sont généralement plus chers que les médicaments à dosage plus faible.
Effets « combinaison de médicaments »
6. Effet « médicament existant »
Cet effet illustre l'incidence des variations des parts de marchés entre les molécules (ingrédients actifs) disponibles pendant les deux périodes analysées. Ce facteur important peut correspondre à des changements constatés dans les tendances de traitement, dans les pratiques de prescription des médecins et dans la prévalence des maladies dans la population. Cet effet illustre la transition entre les médicaments, de même que les variations des parts de marchés entre les différentes catégories et sous-catégories thérapeutiques. La méthodologie proposée permet de différencier ces composantes en décomposant davantage cet effet dans les niveaux des catégories et des sous-catégories thérapeutiques, comme cela est expliqué en détail dans la section 5 du présent rapport.
7. Effet « médicament retiré du formulaire »
Cet effet illustre l'incidence des variations dans l'utilisation alors que l'on se détourne des médicaments qui ne sont plus utilisés au cours de la deuxième période. On s'attend à ce que sa contribution soit minimale, à moins que l'on ne retire des médicaments importants (p. ex. Vioxx).
8. Effet « nouveau médicament »
Cet effet illustre l’incidence des variations de l'utilisation alors que l'on adopte des médicaments qui ont fait leur apparition sur le marché au cours de la deuxième période. Étant donné que de nouveaux médicaments sont constamment lancés sur le marché, cela peut constituer un facteur de coût important. Les nouveaux médicaments moins coûteux permettront des économies et les nouveaux médicaments plus coûteux entraîneront des augmentations de coûts. La valeur de ce facteur équivaudrait à l'effet net de ces deux forces opposées.
Effets « démographiques »
Si des données contiennent des renseignements démographiques, il est possible d'isoler les composantes démographiques de l'effet général « nombre des ordonnances ». Ces facteurs peuvent avoir une incidence sur le coût des médicaments et sur les dépenses en honoraires professionnels. La section 4 du rapport examine les effets « démographiques » du coût des médicaments et des frais d'exécution des ordonnances.
9. Effet « population »
Cet effet illustre la mesure à laquelle la variation progressive de la taille de la population contribue à la variation du coût des médicaments ou des frais d'exécution des ordonnances.
10. Effet « vieillissement »
Cet effet illustre l'incidence des variations de la distribution de la population par groupes d'âge. Une population plus âgée est généralement associée à une augmentation de l'utilisation de médicaments et des coûts. Par conséquent, les changements démographiques pour passer à une population plus vieille ou plus jeune ont respectivement une incidence positive et négative sur les dépenses en médicaments d'ordonnance. Soulignons par ailleurs qu'à défaut de changements majeurs dans la population (p. ex. l'introduction d'un nouveau régime d'assurance-médicaments), cet effet devrait avoir une incidence limitée sur les coûts d'une année à l'autre et qu'il se peut qu'une incidence notable ne puisse être observée qu'au terme d'une longue période (p. ex. 5 ou 10 ans).
11. Effet « sexe »
Cet effet illustre l'incidence des changements de la répartition selon le sexe dans la population. Le coût des médicaments peut varier selon le sexe en raison des différences dans la prévalence des maladies et dans les tendances en matière d'utilisation de médicaments. Comme dans le cas de l'effet « vieillissement », à défaut de changements majeurs touchant la population, cet effet devrait être considéré comme négligeable et pourrait être regroupé avec les effets décrits précédemment dans un effet « vieillissement et sexe ».
2.2 Facteurs associés aux frais d'exécution des ordonnances
La présente section présente trois facteurs associés aux frais d'exécution des ordonnances. La méthodologie et les résultats relatifs aux facteurs associés aux dépenses en honoraires professionnels ont été publiés dans un précédent rapport du SNIUMP (CEPMB, 2011).
1. Effet « frais d'exécution des ordonnances »
Cet effet illustre l'incidence des variations du coût moyen des frais d'exécution des ordonnances.
2. Effet « nombre d'ordonnances »
Cet effet illustre l'incidence associée aux variations du nombre moyen d'unités d'un médicament administré par ordonnance. Soulignons que cet effet augmente aussi le coût des médicaments, mais qu'il entraîne le résultat contraire de l'effet abordé à la section 2.1. Une hausse de cette mesure contribue de façon négative à l'augmentation des dépenses liées aux frais d'exécution des ordonnances étant donné qu'il faut un plus petit nombre d'ordonnances pour délivrer une quantité constante de médicaments.
3. Effet « volume des médicaments »
Cet effet illustre l'incidence associée à la variation du nombre d'unités d'un médicament administré aux patients pendant les deux périodes analysées.
Soulignons que si les renseignements sur l'approvisionnement quotidien sont disponibles et rapportés de façon fiable dans les données, ils peuvent remplacer les renseignements sur les « unités » dans le cadre de calculs des facteurs associés aux frais d'exécution. Dans tels cas, l'effet « nombre d’ordonnances » et l'effet « volume des médicaments » deviendraient l'effet « durée de l'ordonnance » et un effet « volume » tenant compte des renseignements sur l'approvisionnement quotidien.
Si les données contiennent des renseignements démographiques, les composantes démographiques peuvent être isolées de l'effet général « volume des ordonnances » et les trois effets « démographiques » énumérés ci-dessus peuvent être calculés pour la composante des frais d'exécution des ordonnances des dépenses en médicaments sur ordonnance.
2.3 Facteurs associés à la partie des coûts versée par le régime d'assurance-médicaments
En plus de contenir des renseignements sur les coûts en médicaments et les frais d'exécution d'ordonnances, certaines bases de données administratives peuvent comporter des renseignements sur la partie des dépenses en médicaments d'ordonnance qui est remboursée par les régimes d'assurance-médicaments (qu'ils soient publics ou privés), ainsi que sur la partie restante payée par le bénéficiaire. Le présent rapport examine aussi les facteurs qui influent sur les montants versés par le régime d'assurance et les montants versés par le bénéficiaire.
2.4 Effets croisés
Les effets pris isolément et dérivés au moyen de la méthodologie proposée dans le présent rapport expliquent la plupart, mais non la totalité, des variations des dépenses en médicaments d'ordonnance. Il en est ainsi parce que l'effet de chacun des facteurs est déterminé en supposant que tous les autres facteurs demeurent inchangés pendant la période analysée. En réalité, cependant, nombreux sont les facteurs qui changent simultanément, ce qui engendre des effets résiduels ou des effets croisés.
Les effets croisés peuvent être déclarés séparément ou être répartis parmi les effets pris isolément. Une explication détaillée est fournie à la section 3. Plus le nombre d'effets pris isolément est élevé, plus leur interaction entraînera des effets croisés.
L'existence d'effets croisés ne constitue pas une faille du cadre normalisé des facteurs de coût, mais plutôt l'inévitable résultat des interactions entre les changements aux données d'entrée.
3. Exigences et approches de base
Entreprendre une analyse des facteurs de coût exige une compréhension des mécanismes de base de la méthodologie : ce qui est nécessaire à son fonctionnement et la façon dont elle fonctionne. La section 3.1 examine les sources de données et les éléments de données nécessaires. La section 3.2 examine la logique sous-jacente de l’indice de Laspeyres dans la méthodologie proposée. La section 3.3 examine les approches de rechange que sont la décomposition de Paasche et la décomposition idéale de Fisher.
3.1 Exigences en matière de données : sources et éléments de données
Sources
Les bases de données administratives, qui comportent des renseignements sur les médicaments expédiés, vendus, administrés ou remboursés au Canada, peuvent être utilisées pour déterminer les facteurs de coût. Celles-ci comprennent les données sur les régimes publics et privés d’assurance-médicaments, les données sur les ventes dans les pharmacies, les données sur les expéditions de médicaments, les données provenant des hôpitaux, etc. Ces bases de données contiennent généralement des renseignements sur les médicaments et sur la quantité de médicaments, sur les mesures des prix et des coûts et certaines données démographiques.
De nombreuses bases de données comprennent le numéro d’identification du médicament (DIN) émis par Santé Canada. Si le DIN est disponible, les données peuvent être liées aux bases de données et à la Base de données sur les produits pharmaceutiques (BDPP)1. La BDPP contient des renseignements spécifiques très détaillés sur les médicaments homologués au Canada, y compris le nom de marque, le nom des molécules ou des ingrédients, le dosage, la forme galénique, l’emballage, le fabricant, la classification thérapeutique, etc.
Une compréhension approfondie des bases de données disponibles et de leurs limites est nécessaire à la réussite de l’analyse. La qualité des données doit être vérifiée et validée avant de procéder à l’analyse et d’établir le rapport des résultats. De plus, il est nécessaire de faire appel à une personne possédant une expertise dans l’analyse des données et connaissant bien le logiciel utilisé pour analyser les grands ensembles de données.
Éléments de données
Pour mener les analyses des facteurs de coût, il est nécessaire de disposer des éléments de données fondamentaux suivants relativement à chacune des deux périodes comparées : (i) des renseignements sur chacun de ces médicaments; (ii) la quantité et les parts de marché correspondantes de chacun des médicaments et (iii) les coûts ou les prix des médicaments correspondants. Si on dispose de renseignements démographiques, il est possible de les intégrer à la méthodologie afin de permettre une meilleure compréhension des facteurs de coûts.
Renseignements sur le médicament
Les renseignements sur le médicament comprennent une grande variété de caractéristiques, y compris le DIN, le nom de marque, le nom des molécules ou des ingrédients, le dosage, la forme galénique, le format d’emballage, la catégorie et la sous-catégorie thérapeutique, le fabricant et une mention indiquant si le médicament est vendu sous un nom de marque ou un nom générique. La méthodologie proposée dans le cadre de la présente étude exige les renseignements suivants sur le médicament : le nom des molécules ou des ingrédients, le dosage, la forme galénique de même qu’une mention indiquant si le médicament est vendu sous un nom de marque ou un nom générique.
Quantité
La quantité de médicaments peut être mesurée de différentes façons : le nombre d’ordonnances, d’unités physiques ou de jours de traitement.
Le nombre d’ordonnances est une mesure générale de la quantité de médicaments utilisée. Bien qu’elle présente l’avantage d’être cumulées pour les médicaments, elle comporte le désavantage de dissimuler le volume réel d’unités physiques (taille d’ordonnances) de même que le prix unitaire et le coût des médicaments (prix des médicaments). Par conséquent, bien qu’il soit utilisé comme mesure de quantité indépendante des analyses des facteurs de coût, le nombre d’ordonnances est habituellement utilisé de concert avec le nombre d’unités physiques.
Le nombre d’unités physiques détermine le prix ou le coût au niveau de l’unité, ainsi que le nombre moyen d’unités par ordonnance. Sans les renseignements sur le nombre d’ordonnances, les unités physiques ne constituent pas une mesure de quantité indépendante utile. Le nombre d’unités n’est généralement pas cumulé entre les médicaments, étant donné que les médicaments sont offerts à des formulations différentes (solides oraux, solutions injectables, onguents, timbres, etc.).
Le nombre de jours de traitement (ou d’approvisionnements quotidiens) peut être disponible dans certaines bases de données administratives et peut être intégré à la méthodologie de décomposition des coûts pour y inclure le niveau de traitement ou la composante de la durée. Toutefois, la fiabilité et la cohérence du processus d’établissement de rapports sur ces données doivent être évaluées avant son utilisation.
La DDD (Defined Daily Dose), la dose thérapeutique quotidienne définie par l’Organisation mondiale de la santé (OMS), est également utilisée pour décomposer les hausses de dépenses relatives aux médicaments (Gerdtham et Lundin, 2004). Cependant, des études précédentes conseillent de faire preuve de prudence dans l’interprétation du coût moyen ou du prix de la DDD (CEPMB, 2010).
Prix ou coût
Cela peut comprendre différentes mesures touchant les ventes ou les coûts des médicaments sur ordonnance : prix des médicaments en différents points de vente (fabricant, grossiste, pharmacie) ou remboursement du coût des médicaments par les régimes d’assurance-médicaments. Ces éléments peuvent illustrer les frais supplémentaires des grossistes et les marges bénéficiaires des pharmacies.
Les dépenses liées aux frais d’exécution des ordonnances peuvent aussi être analysées dans le cadre d’une analyse des facteurs de coût (CEPMB, 2011).
Données démographiques
Certaines bases de données administratives (p. ex. les données des régimes publics ou privés d’assurance-médicaments) peuvent recueillir des données démographiques, comme le nombre de personnes qui utilisent le médicament pendant les deux périodes de temps, de même que leur âge et leur sexe. Les analyses des facteurs de coût peuvent intégrer ces données démographiques de haut niveau.
3.2 La décomposition des coûts de base
La méthodologie des facteurs de coût proposée dans le présent rapport utilise l’approche de Laspeyres pour décomposer les coûts en deux déterminants ou facteurs : le prix et la quantité. Cette méthode est utilisée dans le cadre d’autres études du CEPMB relativement aux dépenses en médicaments d’ordonnance (CEPMB, 2004, 2006 et 2011).
Le principe fondamental sur lequel repose la décomposition des coûts s’applique à de nombreux secteurs de l’analyse électronique. Il existe de nombreux documents sur les indices de prix et de quantité et la façon dont les dépenses peuvent être divisées entre les composantes de prix et de quantité (Berndt et coll., 2000; Diewert, 2001; Division de la statistique des Nations Unies, 2008).
En comparant les deux périodes de temps, l’approche de Laspeyres isole l’effet de variation d’un facteur précis (p. ex. le prix) en maintenant l’autre facteur (p. ex. la quantité) constant à sa valeur pendant la période de référence. Les nombreux facteurs de coût associés aux dépenses en médicaments d’ordonnance peuvent être isolés et quantifiés si on étend cette approche à un cadre multifactoriel.
La présente section examine l’indice de Laspeyres et décrit le modèle simple constitué d’un produit et de deux facteurs : le prix et la quantité. La prochaine section examine les approches de rechange, à savoir l’indice de Paasche et l’indice idéal de Fisher. Une discussion plus approfondie concernant ces trois index est présentée aux annexes 1, 2 et 3, respectivement.
Décomposition des coûts de base au moyen de l'approche de Laspeyres
Supposons qu’une certaine variable monétaire X (p. ex. les dépenses en médicaments) représente le produit d’un prix P et la mesure de la quantité physique Q. En termes algébriques, cette situation s’exprimerait ainsi :
(1) X = PQ
Supposons aussi que nous disposons d’observations de X, de P et de Q sur deux périodes, une période actuelle (indiquée par l’indice « 1 ») et une période de référence (indiquée par l’indice « 0 »). Il découle de (1) que :
(2.1) X(0) = P(0)Q(0)
(2.2) X(1) = P(1)Q(1)
Supposons finalement que nous souhaitons savoir dans quelle mesure la variation de X entre la période de référence et la période en cours peut être attribuée à P et à Q. Une approche commence par faire observer que le prix de la période en cours (ou la quantité) est égal à son équivalent de la période de référence additionné à la variation de prix (ou de la quantité) qui a été observée entre les deux périodes :
(3.1) P(1) = P(0) + [P(1) – P(0)]
(3.2) Q(1) = Q(0) + [Q(1) – Q(0)]
En substituant (3.1) et (3.2) dans (2.2), on obtient :
(4) X(1) = {P(0) + [P(1) – P(0)]}{Q(0) + [Q(1) – Q(0)]}
En développant le deuxième membre de l’équation (4), cela donne :
(5) X(1) = P(0)Q(0) + [P(1) – P(0)]Q(0) + P(0)[Q(1) – Q(0)] + [P(1) – P(0)][Q(1) – Q(0)]
En soustrayant X(0) des deux membres de l’équation (5) tout en soulignant (2.1), on obtient :
(6) X(1) – X(0) = [P(1) – P(0)]Q(0) (Effet « prix »)
+ P(0)[Q(1) – Q(0)] (Effet « quantité »)
+ [P(1) – P(0)][Q(1) – Q(0)] (Effet croisé)
Les trois termes du deuxième membre de l’équation (6) constituent une décomposition possible de la variation de dépense :
Effet « prix » : Le premier terme du deuxième membre de l’équation (6) est appelé l’effet du prix et constitue un indice de prix de Laspeyres2 exprimé en tant que différence plutôt que sous la forme d’un ratio. Cet effet mesure l’incidence sur X de la variation du prix entre la période de référence et la période en cours en évaluant l’incidence par rapport à la quantité de la période de référence Q(0). Il fait appel à une approche prospective en fournissant une réponse précise à la question :
« Dans quelle mesure X aurait-il changé entre la période de référence et la période en cours si le prix avait changé, mais pas la quantité? »
Effet « quantité » : Le deuxième terme du deuxième membre de l’équation (6) est appelé l’effet de la quantité et constitue un indice de quantité de Laspeyres exprimé en tant que différence plutôt que sous la forme d’un ratio. Cet effet mesure l’incidence sur X de la variation de la quantité entre la période de référence et la période en cours en évaluant l’incidence par rapport au prix de la période de référence P(0). Il fait appel à une approche prospective en fournissant une réponse précise à la question :
« Dans quelle mesure X aurait-il changé entre la période de référence et la période en cours si la quantité avait changé, mais pas le prix? »
L'effet croisé : Le troisième terme du deuxième membre de l’équation (6) diffère des effets « prix » et « quantité » en ce sens qu’il implique des variations de P et de Q. Il est généralement appelé « l’effet croisé de Laspeyres » et sert à mesurer l’incidence sur X qu’a l’interaction entre la variation de prix et la variation de quantité. L’effet croisé se distingue des effets « prix » et « quantité » et doit être inclus pour que la décomposition tienne pleinement compte de la variation de X.
Le diagramme suivant illustre l’effet « prix », l’effet « quantité » et l’effet croisé. Dans le cas de la période de base, où le prix est exprimé par P(0) et la quantité par Q(0), les dépenses sont représentées par le rectangle blanc. Le prix grimpe pour passer de P(0) à P(1) et la quantité augmente de Q(0) à Q(1) pendant la période en cours. L’augmentation correspondante de X est représentée par les secteurs colorés. Le rectangle vert représente l’effet « prix » (c.-à-d. l’incidence de X sur la variation du prix évalué en Q(0)). Le rectangle mauve représente l’effet « quantité » (c.-à-d. l’incidence de X sur la variation de la quantité évaluée en P(0)). Le rectangle orange, ayant une largeur de [Q(1) – Q(0)] et une hauteur de [P(1) – P(0)], complète le secteur de la variation de dépenses. Le dernier rectangle représente l’effet croisé (c.-à-d. l’incidence de X sur l’interaction entre la variation du prix et la variation de la quantité).

La décomposition de Laspeyres abordée précédemment décrit le cas simple d’un seul produit pour lequel la dépense est une fonction de deux facteurs : le prix et la quantité. Une analyse des facteurs de coût dans le monde réel porte habituellement sur plusieurs produits pour lesquels la dépense en médicaments est une fonction de multiples facteurs. Ce genre de cadre de travail est traité en détail à l’annexe 1.
3.3 Approches de rechange
Bien que la présente étude propose une approche basée sur la décomposition de Laspeyres, d’autres approches valides peuvent être utilisées pour effectuer les analyses de facteurs de coût, comme l’indice de Paasche et l’indice idéal de Fisher. Ces indices de prix et de quantité ont leurs propres limites et le choix de l’approche devrait dépendre du champ d’application de la recherche et de l’application proposée des résultats. Voici un bref examen des trois approches.
Approche de Laspeyres
Comme mentionné précédemment, l’approche de Laspeyres est une approche prospective qui évalue chacun des facteurs de coût en maintenant les autres facteurs à leurs valeurs pendant la période de référence. Il faudrait l’employer pour répondre au genre de question suivante :
« Quelle est la part des dépenses effectuées cette année qui est strictement attribuable à des prix plus élevés? »
Cette approche devrait s’employer lorsque les effets « prix » et « quantité » doivent tenir compte de la hausse réelle et globale du prix et de la quantité, respectivement, c.-à-d. en tenant compte de l’effet croisé isolément. (Pour une description plus détaillée, voir l’annexe 1.)
Approche de Paasche
En revanche, l’approche de Paasche est une approche rétrospective qui évalue chacun des facteurs de coût en maintenant les autres facteurs à leurs valeurs pendant la période en cours. Il faudrait l’employer pour répondre au genre de question suivante :
« Jusqu'à quel point la dépense aurait-elle été moindre cette année aux prix de l’année dernière? »
Cette approche peut être utilisée en conjugaison avec l’approche de Laspeyres dans la décomposition de type Fisher. (Pour une description plus détaillée, voir l’annexe 2.)
Approche idéale de Fisher
L’approche idéale de Fisher est un mélange de l’approche prospective de Laspeyres et de l’approche rétrospective de Paasche. La décomposition idéale de Fisher, contrairement à l’approche de Laspeyres, ne ventile pas chacun des effets croisés, mais les distribue également entre chacun des facteurs en jeu. Par conséquent, on la considère comme l’attribution intégrale de l’approche axée sur les dépenses. Le même résultat peut être obtenu en répartissant en parts égales les effets croisés de Laspeyres en fonction de chacun des facteurs. (Voir l’algorithme décrit à l’annexe 4.)
L’approche idéale de Fisher attribue l’intégralité des dépenses aux effets pris isolément, ainsi chacun des effets illustre les interactions avec tous les autres effets. Cette approche ne devrait être employée que lorsqu’une répartition à parts égales des effets croisés est jugée appropriée.
La distribution en parts égales des effets croisés peut être perçue comme arbitraire, mais elle n’est pas plus arbitraire que le fait d’attribuer l’intégralité d’un effet croisé à un seul facteur. On pourrait aller plus loin et soutenir que cette approche a la propriété séduisante de l’impartialité : faute de sérieux motifs justifiant l’attribution d’un plus grand nombre d’effets croisés à un facteur plutôt qu’à l’autre, il semble approprié d’effectuer un partage égalitaire entre les deux facteurs.
Si les facteurs de dépenses varient indépendamment l’un de l’autre, il est raisonnable de supposer que les effets croisés devraient être répartis en parts égales. Cependant, ce n’est pas toujours le cas. Supposons, par exemple, que la quantité de médicaments n’ait augmenté qu’en raison du lancement d’un médicament générique et du rabais sur le prix qu’il offre. Si l’objectif est d’attribuer l’intégralité de l’effet croisé à l’effet de la quantité et à l’effet de la substitution par un médicament générique, il serait alors logique d’attribuer cet effet dans son intégralité à l’effet de la substitution par un médicament générique. Dans ce cas, l’effet de la substitution par un médicament générique illustrerait non seulement le prix des médicaments génériques (devant être un effet négatif), mais également l’augmentation de l’utilisation (devant être un effet positif). L’effet net sera positif ou négatif en fonction de l’incidence qui est la plus forte.
Et si l’on devait tenir compte de trois facteurs? Supposons, par exemple, qu’un modèle tenait compte des dépenses effectuées en fonction du produit du prix, de la quantité par requérant et de la population de requérants. Dans ce cas, il y aurait quatre effets croisés de Laspeyres à calculer : trois effets doubles mettant en jeu des variations de deux des trois facteurs, ainsi qu’un effet triple mettant en jeu tous les trois facteurs. L’approche de décomposition idéale de Fisher requiert que chacun des doubles effets croisés soit divisé également entre les deux facteurs contribuant à la variation. De même, le triple effet croisé devrait être divisé également entre tous les trois facteurs.
Dans une méthodologie multifactorielle complexe de décomposition du coût, comme celle qui est proposée dans la présente étude, il y aura un grand nombre d’interactions entre chacun des facteurs, pour correspondre aux effets croisés qu’ils soient doubles, triples, quadruples, etc. Une discussion portant sur ces effets croisés, ainsi que sur les formules correspondantes, est présentée aux annexes 4 à 8. La répartition à parts égales de ces effets croisés entre chacun des facteurs afin d’en arriver à une pleine attribution peut être un exercice très complexe.
Voilà pourquoi nous recommandons l’approche de Laspeyres. Dans le cas présent, les effets pris isolément seront signalés tel que décrit à la prochaine section (section 4) et la variation des dépenses qui reste inexpliquée en raison des effets croisés sera signalée séparément.
1 http://www.hc-sc.gc.ca/dhp-mps/prodpharma/databasdon/index-fra.php
2 L’appellation « Laspeyres » provient de la célèbre méthodologie de l’indice des prix de Laspeyres. L’indice des prix à la consommation est peut-être le meilleur exemple d’un indice des prix de Laspeyres. La méthodologie de Laspeyres permet d’évaluer les tendances générales des prix en effectuant le suivi du coût d’un panier de biens et de services déterminé, en fonction du temps.
4. Formules pour le calcul des facteurs de coût associés aux dépenses en médicaments d'ordonnance
La présente section fournit les formules de calcul des facteurs de coût associés aux dépenses en médicaments d’ordonnance, de même que les exigences en matière de données et les notes méthodologiques qui peuvent être appliquées pour quantifier les facteurs associés aux coûts des médicaments (section 4.1) et les facteurs associés aux frais d’exécution (section 4.2) La section 4.3 fournit les formules permettant de déterminer les effets démographiques du coût des médicaments et des frais d’exécution des ordonnances. La dernière section (section 4.4) examine les facteurs associés à partie des coûts versée par le régime d’assurance-médicaments.
Comme nous l’avons vu précédemment, la méthodologie proposée repose conceptuellement sur l’approche de Laspeyres de décomposition des coûts. L’analyse peut se limiter à cette approche et aux effets croisés indiqués séparément. Par ailleurs, l’approche idéale de Fisher peut aussi être employée en attribuant l’ensemble des effets croisés de Laspeyres aux facteurs pris isolément. L’algorithme décrit à l’annexe 4 présente le cadre nécessaire pour ce faire.
4.1 Facteurs associés aux coûts des médicaments
Les facteurs associés aux coûts des médicaments sont présentés ci-dessous dans le contexte de trois grandes catégories, tel que décrit à la section 2.1.
Effets « prix » :
- Effet « variations de prix »
- Effet « substitution par des médicaments génériques »
Effets « volume » :
- Effet « volume des ordonnances »
- Effet « nombre d’ordonnances »
- Effet « dosage et forme galénique des médicaments »
Effets « combinaison de médicaments » :
- Effet « médicament existant »
- Effet « médicament retiré du formulaire »
- Effet « nouveau médicament »
Au minimum, il importe de présenter les éléments de données suivants relativement aux deux périodes de temps :
blank
| Molécule (ingrédient actif) |
|
| Indication de marque ou générique |
Propriétés médicamenteuses |
| Dosage et forme galénique3 |
|
blank
| Coût, ventes ou prix du médicament |
|
| Unités (nombre de comprimés, de gélules, etc.) |
Mesures |
| Nombre d’ordonnances |
|
Les mesures sont regroupées en fonction de leurs propriétés, et non de leur DIN, afin d’éliminer les détails inutiles comme les formats d’emballage et les données relatives au fabricant.
De plus, on doit attribuer à toutes les molécules un statut « médicament existant-médicament retiré du formulaire-nouveau médicament » en fonction du fait qu’elles étaient utilisées, ou non, au cours des deux périodes visées par la comparaison :
- Médicaments existants: les molécules étaient utilisées au cours des deux périodes.
- Médicaments retirés du formulaire : les molécules étaient utilisées au cours de la première période, mais pas pendant la deuxième.
- Nouveaux médicaments : les molécules n’étaient pas utilisées au cours de la première période, mais on a commencé à les utiliser pendant la deuxième.
Le regroupement des molécules par statut « médicament existant-médicament retiré du formulaire-nouveau médicament » devrait s’effectuer en fonction de l’utilisation réelle, telle qu’indiquée dans les données, et non en fonction de la date de l’avis de conformité, de la date du lancement, de la date du formulaire ou de n’importe quelle autre date.
Mentionnons que, dans le cadre de la présente analyse, le mot produit désigne toute combinaison unique des propriétés suivantes : les combinaisons de dosage et de formes galéniques (s), l’indication de marque ou de générique (b), les molécules (m) et le statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e).
Les coûts ou les ventes de médicaments dans un marché à produits multiples au cours d’une période de temps donnée peuvent être exprimés comme le produit du coût moyen par unité, le nombre moyen d’unités par ordonnance et le nombre d’ordonnances pour un produit, additionnés pour tous les produits :
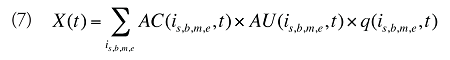
où :
is,b,m,e est un produit présentant une combinaison dosage et forme galénique (s), une indication de marque ou générique (b), une molécule (m) et un statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
t est une constante correspondant à la valeur au cours de la période visée par l’analyse
X(t) est le montant total de la dépense en médicaments ou des ventes de ces médicaments au cours de la période t
AC(is,b,m,e,t) est le coût ou le prix moyen par unité physique du produit is,b,m,e au cours de la période t
AU(is,b,m,e,t) est le nombre moyen d’unités (quantités physiques) par nombre d’ordonnances pour le produit is,b,m,e au cours de la période t
q(is,b,m,e,t) est le nombre d’ordonnances pour le produit is,b,m,e au cours de la période t
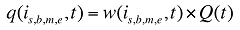
où :
w(is,b,m,e,t) est la part is,b,m,e du produit du volume total (exprimé en ordonnances) au cours de la période t
Q(t) est le nombre total des ordonnances exécutées au cours de la période t
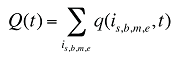
(8)
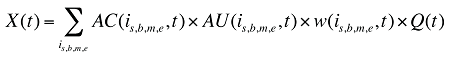
Chaque part w(is,b,m,e,t) pris isolément peut être décomposée en parts multiples, de la façon suivante :
(9)
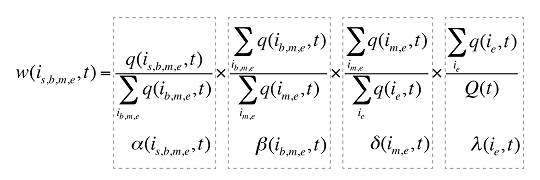
où :
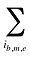 est la somme de la quantité d’ordonnances pour tous les produits i partageant les mêmes indications de marque ou de générique (b), les mêmes molécules (m) et le même statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
est la somme de la quantité d’ordonnances pour tous les produits i partageant les mêmes indications de marque ou de générique (b), les mêmes molécules (m) et le même statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
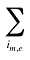 est la somme des quantités de tous les produits i partageant les mêmes molécules (m) et statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
est la somme des quantités de tous les produits i partageant les mêmes molécules (m) et statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
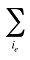 est la somme des quantités de tous les produits i partageant le même statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
est la somme des quantités de tous les produits i partageant le même statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
a(is,b,m,e,t) est la part de la quantité du produit i sur la somme des quantités de tous les produits partageant les mêmes indications de marque ou générique (b), molécules (m) et statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
b(ib,m,e,t) est la part de la somme des quantités de produits i partageant les mêmes indications de marque ou générique (b), les mêmes molécules (m) et le même statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e) sur la somme des quantités de tous les produits partageant les mêmes molécules (m) et le même statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
d(im,e,t) est la part de la somme des quantités de produits i partageant les mêmes molécules (m) et le même statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e) sur la somme des quantités de tous les produits partageant le même statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e)
l(ie,t) est la part de la somme des quantités de produits i partageant le même statut « médicament existant-médicament retiré du formulaire-nouveau médicament » (e) sur la quantité totale de tous les produits au cours de cette période.
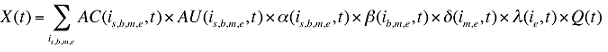
La variation de la valeur totale des coûts des médicaments au cours de la période 1 par rapport à la période 0 est :
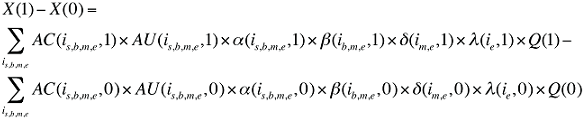
Cette formule peut être exprimée sous la forme suivante, en isolant chacun des effets qui suivent :
Formule 1. Formule de décomposition des coûts – Facteurs associés aux coûts des médicaments

où
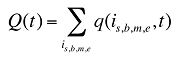
est calculé pour l’ensemble des médicaments existants, des médicaments retirés du formulaire et des nouveaux médicaments et q(is,b,m,e,t) est le nombre d’ordonnances pour le produit is,b,m,e au cours de la période t
où :
 est la somme de tous les médicaments existants
est la somme de tous les médicaments existants
 est la somme de l’ensemble des médicaments existants et des médicaments retirés du formulaire, et
est la somme de l’ensemble des médicaments existants et des médicaments retirés du formulaire, et
 est la somme de l’ensemble des médicaments sur le marché et des nouveaux médicaments
est la somme de l’ensemble des médicaments sur le marché et des nouveaux médicaments
Les cinq premiers effets de la formule 1 ne sont calculés que pour les médicaments existants, puisqu’ils prendraient la valeur de zéro dans le cas des médicaments retirés du formulaire et des nouveaux médicaments.
L’effet « médicament retiré du formulaire » et l’effet « nouveau médicament » observés dans la formule 1 peuvent être combinés en un seul et même effet appelé « médicament retiré du formulaire–nouveau médicament » et englobant tous les deux :

Précisons que l’effet « médicament retiré du formulaire » ne touche que les médicaments existants et les médicaments retirés du formulaire. Le terme l(i,1) prend la valeur de 1 dans le cas des médicaments existants et la valeur de 0 dans le cas des médicaments retirés du formulaire, puisqu’il n’y a pas de médicaments retirés du formulaire à la période 1. De même, l’effet « nouveau médicament » est limité aux médicaments existants et aux nouveaux médicaments. Le terme l(i,1) prend la valeur de 1 dans le cas de médicaments existants et la valeur de 0 dans le cas de nouveaux médicaments. Étant donné que les nouveaux médicaments ne sont pas associés à une valeur pour la période 0, on devrait utiliser les valeurs de la période 1. L’annexe 9 donne un exemple de la façon dont sont décomposés les effets « médicament existant », « médicament retiré du formulaire » et « nouveau médicament ».
En ce qui a trait à la formule 1, mentionnons que s’il est impossible d’obtenir une valeur requise pour une période de temps, il serait préférable de plutôt utiliser la valeur de l’autre période de temps. Cela peut se produire étant donné que les dosages et les formes galéniques de quelques-unes des molécules existantes peuvent être utilisés sporadiquement dans l’une ou l’autre des périodes.
Les effets croisés du médicament sont composés de 120 effets combinés, comme mentionné à l’annexe 5.
4.2 Facteurs associés aux frais d’exécution des ordonnances
Les facteurs associés aux frais d’exécution des ordonnances, tels que mentionnés à la section 2.2, sont les suivants :
- Effet « frais d’exécution des ordonnances »
- Effet « nombre d’ordonnances »
- Effet « volume des médicaments »
Au minimum, il importe de présenter les éléments de données suivants pour les deux périodes de temps :
blank
| Molécule (ingrédient actif) |
Propriétés médicamenteuses |
| Dosage et forme galénique4 |
|
blank
| Dépenses liées aux frais d’exécution des ordonnances |
|
| Unités (nombre de comprimés, de gélules, etc.) |
Mesures |
| Nombre d’ordonnances |
|
Les mesures associés aux médicaments sont regroupées en fonction des propriétés de ces derniers, et non de leur DIN, afin d’éliminer les détails inutiles comme les formats d’emballage et les données relatives au fabricant.
Soulignons que, dans le cadre de la présente analyse, le mot produit désigne toute combinaison de ses propriétés : les molécules, le dosage et la forme galénique.
Les dépenses liées aux frais d’exécution des ordonnances peuvent s’écrire de la façon suivante :
(10) F(t) = AF(t)×Q(t)
où :
F(t) est le total des dépenses liées aux frais d’exécution des ordonnances au cours de la période t
AF(t) est la moyenne des frais d’exécution par ordonnance au cours de la période t
Q(t) est le nombre total d’ordonnances au cours de la période t
À son tour, le nombre d’ordonnances peut s’exprimer comme une fonction des unités administrées:
(11)
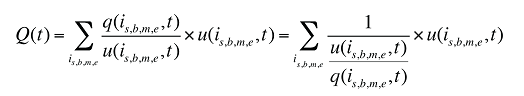
où :
q(is,b,m,e,t) est le nombre d’ordonnances du produit is,b,m,e au cours de la période t
u(is,b,m,e,t) est le nombre d’unités du produit is,b,m,e au cours de la période t
où :
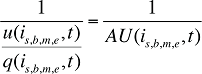
AU(is,b,m,e,t) est le nombre moyen d’unités par quantité d’ordonnances pour le produit is,b,m,e au cours de la période t
Ce terme est inversement proportionnel au nombre d’ordonnances. Plus il est élevé, moins on administre d’unités de médicaments par ordonnance.

Formule 2. Formule de décomposition des coûts – Facteurs associés aux frais d’exécution des ordonnances

Effets croisés des frais d’exécution des ordonnances
Les effets croisés des frais d’exécution des ordonnances sont composés de quatre effets combinés, dont le détail apparaît à l’annexe 7.
Cette méthodologie utilise des frais d’exécution d’ordonnance moyens pour déterminer l’effet « frais d’exécution des ordonnances ». Les frais d'exécution d'ordonnance peuvent varier d’une province à l’autre en fonction du montant remboursé par les régimes d'assurance publics et peuvent également varier selon le fait qu’une pharmacie est située en zone urbaine, rurale ou éloignée.
Les autres honoraires professionnels pour les services et les interventions concernant la gestion des médicaments peuvent aussi être indiqués dans les données administratives. Il peut s’agir des frais exigés pour le renouvellement d’ordonnances, pour les activités d’évaluation et d’adaptation, pour la substitution thérapeutique, pour l’examen des médicaments, pour le refus de délivrer ou de remplir une ordonnance, etc. Il faut cerner ces frais et les écarter de l’analyse des facteurs associés aux frais d'exécution d'ordonnances.5
Soulignons que si les renseignements sur l’approvisionnement quotidien sont disponibles et rapportés de façon fiable dans les données, ils peuvent remplacer les renseignements sur les « unités » dans le cadre de calculs des facteurs associés aux frais d’exécution. Dans tels cas, l’effet « nombre d’ordonnances » et l’effet « volume des médicaments » deviendraient l’effet « durée de l’ordonnance » et un effet « volume » tenant compte des renseignements sur l’approvisionnement quotidien.
4.3 Effets « démographiques » des coûts en médicaments et des frais d’exécution des ordonnances
Si les renseignements pertinents sont disponibles, les effets « démographiques » peuvent être isolés des effets « volume » correspondant aux composantes du coût des médicaments et des frais d’exécution des dépenses en médicaments d’ordonnance. Les effets « démographiques » englobent les trois effets suivants (décrits à la section 2) :
- Effet « population »
- Effet « vieillissement »
- Effet « sexe »
Les effets « démographiques » peuvent être extraits si les données sur les dépenses par rapport au nombre d’ordonnances et celles sur la taille de la population par rapport à l’âge et au sexe sont disponibles. Les éléments de données suivants peuvent être utilisés pour les deux périodes :
blank
| Âge (tranches d’âge de 5 ou 10 ans recommandées) |
Caractéristiques démographiques |
| Sexe |
|
blank
| Taille de la population (nombre de patients, de requérants, de bénéficiaires, etc.) |
|
| Coûts des médicaments (ventes) ou dépenses en frais d’exécution des ordonnances |
Mesures |
| Nombre d’ordonnances |
|
Les mesures doivent être regroupées en fonction de la démographie (âge et sexe). Les renseignements sur l’âge peuvent se présenter sous la forme de groupes d’âge; plus les renseignements sur l’âge sont granulaires, plus le calcul de l’effet « vieillissement » sera précis.
Effets « démographiques » des coûts en médicaments
À l’échelle de la population, les coûts en médicaments ou les ventes de ces derniers au cours d’une période donnée dans une population dont l’âge, la répartition des sexes et la taille sont connus, peuvent être exprimés comme le produit du coût moyen par ordonnance, la moyenne du nombre d’ordonnances en fonction de la population et le nombre de patients dans les groupes répartis selon l’âge ou le sexe, additionnés pour tous les groupes :
(12)
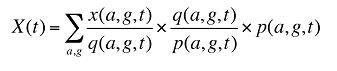
où :
x(a,g,t) est coût des médicaments ou les ventes de médicaments pour le groupe d’âge a et le sexe g au cours de la période t
q(a,g,t) est le nombre d’ordonnances pour le groupe d’âge a et le sexe g au cours de la période t
p(a,g,t) est la population du groupe d’âge a et du sexe g au cours de la période t
Le dernier terme peut être ainsi exprimé :
(13)
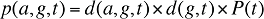
où :
d(a,g,t) est la part de la population du groupe d’âge a et du sexe g par rapport à la population totale de sexe g au cours de la période t
d(g,t) est la part de la population de sexe g par rapport à la population totale au cours de la période t
P(t) est la population totale au cours de la période t
(14)
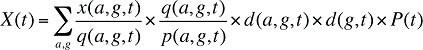
En maintenant constant aux valeurs de la période de référence le coût moyen par ordonnance et le nombre moyen d’ordonnances en fonction de la population, il est possible d’isoler les effets « démographiques » des coûts en médicaments de la façon suivante :
Formule 3. Formule de décomposition des coûts – Effets « démographiques » des coûts en médicaments

Effets « démographiques croisés »
Les effets « démographiques croisés » sont composés de quatre effets combinés, dont le détail apparaît à l’annexe 6.
Si l’on calcule les effets « démographiques » des coûts en médicaments de la façon décrite plus haut, l’effet « volume des ordonnances » de la formule 1 dit être libéré des effets « démographiques » avant que l’on puisse déterminer les effets des médicaments. Pour ce faire, il suffit de remplacer Q(1) par QS(1), qui représente la quantité d’ordonnances pendant la période 1 normalisée en fonction du profil démographique que l’on a utilisé pour la période 0. Le profil démographique renvoie à l’âge (a), au sexe (g) et à la taille de la population (P).
(15)
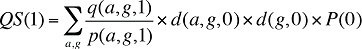
L’effet « volume des ordonnances » calculé au moyen de la variable QS(1) de la formule 1 ne présente pas d’effets « démographiques », il n’illustre que les variations du nombre d’ordonnances dans une population ayant la même répartition des âges et des sexes ainsi que la même taille qu’au cours de l’année de référence.
Effets « démographiques » associés aux frais d’exécution des ordonnances
De même, à l’échelle de la population, les dépenses liées aux frais d’exécution des ordonnances au cours d’une période donnée pour une population dont l’âge, la répartition des sexes et la taille sont connus, peuvent être exprimées comme le produit de la moyenne des frais par ordonnance, la moyenne du nombre d’ordonnances pour chacune des populations et le nombre de patients dans les groupes répartis selon l’âge ou le sexe, additionnés pour tous les groupes :
(16)
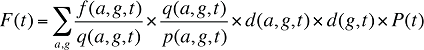
où :
f(a,g,t) représente les dépenses liées aux frais d’exécution des ordonnances pour le groupe d’âge a et le sexe g au cours de la période t
q(a,g,t) est le nombre d’ordonnances pour le groupe d’âge a et le sexe g au cours de la période t
p(a,g,t) est la population du groupe d’âge a et du sexe g au cours de la période t
d(a,g,t) est la part de la population du groupe d’âge a et du sexe g par rapport à la population totale de sexe g au cours de la période t
d(g,t) est la part de la population de sexe g par rapport à la population totale au cours de la période t
P(t) est la population totale au cours de la période t
En maintenant constant aux valeurs de la période de référence le coût moyen par ordonnance et le nombre moyen d’ordonnances en fonction de la population, il est possible d’isoler les effets « démographiques » des dépenses liées aux frais d’exécution des ordonnances de la façon suivante :
Formule 4. Formule de décomposition des coûts – Effets « démographiques » des dépenses liées aux frais d’exécution des ordonnances

Les effets « démographiques croisés » sont composés de quatre effets combinés, dont le détail apparaît à l’annexe 6.
Si l’on calcule les effets « démographiques » des coûts en médicaments de la façon décrite plus haut, l’effet « volume des médicaments » de la formule 2 doit être libéré des effets « démographiques » en remplaçant u(is,b,m,e,1) par us(is,b,m,e,1), qui représente le nombre d’unités normalisé en fonction du profil démographique que l’on a utilisé pour la période 0. Celui-ci est calculé selon le nombre normalisé d’ordonnances, de la façon suivante :
(17)
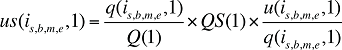
où :
q(is,b,m,e,1) est le nombre de prescriptions du produit is,b,m,e au cours de la période 1
u(is,b,m,e,1) est le nombre d’unités (quantités physiques) du produit is,b,m,e au cours de la période 1
Q(1) est le volume total d’ordonnances au cours de la période 1
QS(1) est le nombre d’ordonnances au cours de la période 1 normalisé en fonction du profil démographique que l’on a utilisé pour la période 0, tel que calculé à l’équation (15). Le profil démographique renvoie à l’âge (a), au sexe (g) et à la taille de la population (P)
(18)
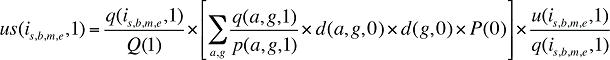
u(is,b,m,e,1) dans la formule 2 est alors remplacé par us(is,b,m,e,1), tel que calculé à l’équation (18). L’effet « volume des médicaments » de la formule 2 calculé au moyen de la variable us(is,b,m,e,1) ne présente pas d’effets « démographiques », il n’illustre que les variations du nombre d’ordonnances dans une population ayant la même répartition des âges et des sexes ainsi que la même taille qu’au cours de l’année de référence.
4.4 Facteurs associés à la partie des coûts versée par le régime d’assurance-médicaments
Certaines bases de données administratives peuvent aussi comporter des renseignements sur la partie des dépenses en médicaments d’ordonnance qui est remboursée par les régimes d'assurance-médicaments (qu'ils soient publics ou privés), ainsi que sur la partie restante payée par les bénéficiaires.
Pour toutes les périodes données, cette relation peut être exprimée ainsi :
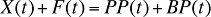
où :
X(t) est le montant total des coûts en médicament au cours de la période t
F(t) est le total des dépenses liées aux frais d’exécution des ordonnances au cours de la période t
PP(t) est le total du montant versé par le régime d'assurance-médicaments et remboursé au cours de la période t
BP(t) est le total du montant versé par le bénéficiaire et remboursé au cours de la période t
Le montant versé par le régime d’assurance-médicaments peut être calculé de la façon suivante :
(19)
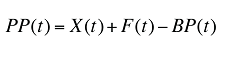
La variation du montant versé par le régime d’assurance-médicaments au cours des deux périodes peut être exprimée ainsi :
(20)
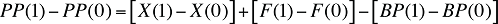
Comme le suggère l’équation ci-dessus, les facteurs associés au montant versé par le régime d’assurance-médicaments équivalent tout simplement à la somme des facteurs associés aux coûts des médicaments et aux frais d'exécution d'ordonnance, à laquelle on soustrait les facteurs associés aux montants payés par les bénéficiaires.
En supposant que des données démographiques sont disponibles, le montant versé par le bénéficiaire peut être exprimé au moyen d’une équation semblable à l’équation (14) :
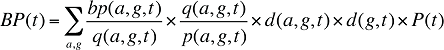
où :
bp(a,g,t) est le montant versé par le bénéficiaire pour le groupe d’âge a et le sexe g au cours de la période t
Formule 5. Formule de décomposition des coûts – Facteurs associés aux montants versés par le bénéficiaire

Effets croisés du montant versé par le bénéficiaire
Les effets croisés du montant versé par le bénéficiaire sont détaillés à l’annexe 8.
Les effets pris isolément de l’équation (20) peuvent être calculés de la façon prévue par les formules 1 à 4 qui tiennent compte des effets « prix », « volume », « combinaison de médicaments », « démographique », etc. Certains effets, comme les effets « volume » et « démographiques » des composantes du coût des médicaments et des frais d'exécution, annuleront en partie les effets correspondants de la composante du montant versé par le bénéficiaire. L’effet net correspondra au facteur associé à la composante du montant versé par le régime d’assurance médicaments.
Une approche plus simple consisterait à décomposer la modification financée par le régime d’assurance médicaments de la même façon que l’on a décomposé le montant versé par le bénéficiaire à la formule 5, en remplaçant l'effet « montant versé par le bénéficiaire pour chacune des ordonnances » par l’effet « montant versé par le régime d’assurance-médicaments pour chacune des ordonnances ». Cela permettra d’obtenir un effet à large portée englobant les effets « prix » et « combinaison de médicaments » de même que certains des effets de volume comme l’effet « nombre d’ordonnances » et l’effet « dosage et forme galénique ».
L'approche proposée dans la présente section présente les changements aux montants versés par le régime d’assurance-médicaments au moyen des facteurs associés au coût des médicaments, aux frais d'exécution d'ordonnance et aux montants versés par les bénéficiaires. Cette approche tient compte de la refonte du régime d’assurance-médicaments (p. ex. les modifications au barème de quote-part déductible) indirectement par l’intermédiaire de la composante versée par les bénéficiaires. La détermination des incidences précises qu’aura la refonte du régime d'assurance-médicaments sur ses dépenses nécessite l’élaboration d’un modèle différent.
3 Le dosage et la forme galénique ne devraient être combinés que dans le cas des produits oraux solides (comprimés, gélules, formulations à libération prolongée, etc.). Les autres formulations (solutions injectables, inhalateurs, timbres, etc.) devraient être traitées comme des produits distincts.
4 Le dosage et la forme galénique ne devraient être combinés que dans le cas des produits oraux solides (comprimés, gélules, formulations à libération prolongée, etc.). Les autres formulations (solutions injectables, inhalateurs, timbres, etc.) devraient être traitées comme des produits distincts.
5 Si l’analyse a pour objectif de cerner les facteurs de dépenses associés aux services professionnels en général, et si les données sont disponibles, il est alors possible de conserver ces frais professionnels aux fins d’analyse. Il est possible de les regrouper en fonction des types de frais (p. ex. les frais d’ordonnance, les frais d’examen des médicaments, les frais de substitution thérapeutique, etc.) et d’ajuster le modèle de facteurs de coût pour déterminer l’effet « frais d’exécution des ordonnances ». Veuillez noter que dans le cas des services et des interventions concernant la gestion des médicaments, les types de frais et les montants faisant l’objet d’un remboursement varient selon les provinces.
Ajustements et améliorations apportés à la méthodologie
L’approche axée sur les facteurs de coût proposée dans la présente étude ne se limite pas qu’aux effets examinés et ne couvre pas non plus l’ensemble de ces effets. La méthodologie peut être adaptée en fonction de la disponibilité des données et des exigences en matière de recherche. La présente section propose des solutions pour diminuer, étendre ou redéfinir les effets que l’on peut saisir à l’aide de la méthodologie de décomposition des coûts.
Les analyses des facteurs de coût ne se limitent pas à la valeur totale des ventes de médicaments ou des dépenses de programmes. Au moyen de la méthodologie normalisée, il est possible de mener des analyses spécialisées des dépenses liées à des groupes de médicaments (p. ex. les catégories thérapeutiques) ou à des segments de la population spécifiques (p. ex. les régimes d’assurance-médicaments ou leurs sous-catégories précises).
De plus, la méthodologie ne se limite pas aux analyses de tendances des variations en matière de ventes ou de dépenses en fonction du temps, elle peut aussi être utilisée dans la réalisation d’analyses couvrant différentes administrations ou de comparaisons internationales visant à décomposer les sources d’écart entre les ventes ou les dépenses en médicaments.
5.1 Réduire le nombre d'effets
Les éléments suivants peuvent être écartés ou remplacés de la méthodologie proposée :
Effets « démographiques »
Il est possible d’écarter un, plusieurs ou l’ensemble des effets « démographiques » de l’analyse. Si tous les effets « démographiques » sont écartés, les formules 1 et 2 peuvent être utilisées sans les formules 3 et 4, respectivement. Si l’on écarte un ou deux effets « démographiques », les formules 1 et 2 seraient utilisées de concert avec une version modifiée des formules 3 et 4.
Effets « prix » et « substitution par un médicament générique »
Si les renseignements disponibles sur le type de médicament ne font pas de distinction entre les produits de marque et les produits génériques, ces deux efforts peuvent être groupés en un seul : un effet « prix » qui comprend la substitution par un médicament générique. Dans ce cas, les attributs requis seraient la molécule, le dosage et la forme galénique. Le prix moyen de chacun des médicaments serait déterminé en fonction du niveau du dosage et de la forme galénique et tiendrait compte du prix et du poids correspondants des médicaments de marque et des médicaments génériques. En l’absence de renseignements permettant de comparer les médicaments de marque aux médicaments génériques, le facteur b(i,k) serait écarté de la formule 1 et l’effet « substitution par un médicament générique » serait intégré à l’effet « prix ».
Effet « volume des ordonnances »
Si les renseignements sur le nombre d’ordonnances ne sont pas disponibles, l’utilisation d’unités physiques comme mesure de quantité indépendante des facteurs de coût aurait deux conséquences :
- L’effet « nombre d’ordonnances » et l’effet « volume des ordonnances » seraient incorporés à l’effet « volume de médicaments ».
- On devrait utiliser le nombre d’unités physiques pour déterminer la part du volume de chacun des produits. Les unités physiques ne sont cependant généralement pas cumulés entre les médicaments, étant donné que les médicaments sont offerts en différents dosages (p. ex. 5, 10, 500 mg) et formulations (solides oraux, solutions injectables, onguents, timbres, etc.). Cela aurait une incidence sur l’effet « combinaison de médicaments », puisque les parts de médicaments signalées comme unités multiples (dans le cas des solides oraux) ou comme unités simples (dans le cas des timbres, des solutions injectables, etc.) pourraient être faussées. Cette limite est atténuée si l’on mène l’analyse sur une seule formulation, p. ex. les solides oraux.
Si l’on utilise les unités physiques pour mesurer la quantité, le facteur AU(is,b,m,e,t) sera éliminé de la formule 1 et le facteur q(is,b,m,e,t) deviendra la quantité exprimée en unités du médicament is,b,m,e au cours de la période t.
De toute évidence, si l’on ne connaît pas le nombre d’ordonnances, il est impossible d’effectuer une analyse des facteurs associés aux frais d’exécution des ordonnances.
Unités physiques
Si les renseignements sur le nombre d’unités physiques ne sont pas disponibles, l’utilisation du nombre d’ordonnances comme mesure de quantité indépendante des modèles des facteurs des coûts des médicaments et des frais d’exécution des ordonnances aurait deux conséquences :
- Pour ce qui est des facteurs qui ont une incidence sur le modèle de coûts des médicaments, l’effet « prix » sera remplacé par un effet « coût moyen par ordonnance », ce qui constituerait une mesure très approximative où entrent en ligne de compte l’effet « prix » et l’effet « nombre d’ordonnances ». Par conséquent, on remplacerait l’équation (7) par la formule combinée ci-dessous, accompagné d’une révision correspondant à la formule 1.
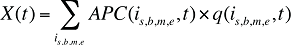
où APC(is,b,m,e,t) est le coût moyen par ordonnance du médicament is,b,m,e au cours de la période t
- Pour ce qui est des facteurs du modèle des frais d’exécution des ordonnances, l’effet « nombre d’ordonnances » et l’effet « volume de médicaments » seraient combinés en un seul effet « volume des ordonnances ». Dans ce modèle, la formule 2 serait fondée sur l’équation (10) et n’inclurait pas la décomposition plus poussée présentée à l’équation (11).
Effets « médicament retiré du formulaire » et « nouveau médicament »
Ces deux effets pris isolément peuvent être combinés en un seul et même effet « médicament retiré du formulaire-nouveau médicament », comme mentionné précédemment.
5.2 Augmenter le nombre d'effets
Effet thérapeutique
L’effet « médicament existant » peut être davantage décomposé en fonction des catégories thérapeutiques et même de sous-catégories. Cela peut se faire en ajoutant une autre composante à la description du produit : la catégorie thérapeutique c.
Par conséquent, il est possible de réviser l’équation (9) en y ajoutant un autre facteur e(ic,e,t), comme suit :
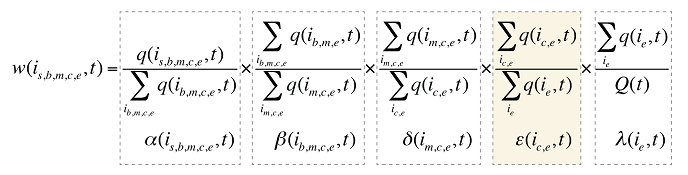
où :
e(ic,e,t) est la part de la somme des quantités des produits i qui présentent la même catégorie thérapeutique (c) et le même statut (e) « médicament existant-médicament retiré du formulaire-nouveau médicament » sur la somme des quantités de tous les produits dont le statut (e) « médicament existant-médicament retiré du formulaire-nouveau médicament » est identique
Un effet de sous-catégorie peut être ajouté à l’effet thérapeutique d’une manière semblable. On peut réviser la formule 1 en conséquence.
Effet « médicament breveté par rapport à médicament non breveté »
Les médicaments peuvent aussi être classés en médicaments brevetés et en médicaments non brevetés. Cela peut être fait en ajoutant un autre terme à l’équation (9) d’une manière semblable à celle décrite plus haut.
Effet « intensité du traitement »
Si les données permettent de déterminer avec exactitude la durée du traitement (en jours) en fonction de la quantité de médicaments utilisés, il est alors possible d’améliorer la méthodologie pour illustrer l’effet « intensité du traitement ».
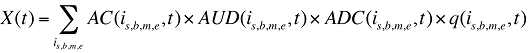
où :
X(t) est le montant total des coûts en médicament au cours de la période t
AC(is,b,m,e,t) est le coût moyen par unité de médicament is,b,m,e au cours de la période t
AUD(is,b,m,e,t) est le nombre moyen d’unités par jour de traitement au médicament is,b,m,e au cours de la période t
ADC(is,b,m,e,t) est le nombre moyen de jours de traitement par ordonnance du médicament is,b,m,e au cours de la période t
q(is,b,m,e,t) est le nombre d’ordonnances du médicament is,b,m,e au cours de la période t
Il est possible de réviser la formule 1 en y ajoutant un nouvel effet qui illustre les variations du nombre d’unités distribuées par jour (intensité du traitement) et en modifiant l’effet du nombre d’ordonnances pour illustrer les variations du nombre de jours de traitement administré par ordonnance au lieu du nombre d’unités physiques administrées par ordonnance.
5.3 Redéfinir les effets
Médicaments à fournisseur exclusif par rapport aux médicaments à plusieurs fournisseurs (MFE–MPF)
L’effet « MFE–MPF » peut remplacer l’effet « substitution par un médicament générique ». Cela peut être réalisé tout simplement en attribuant une désignation de fournisseur exclusif ou de plusieurs fournisseurs à un médicament en remplacement de la catégorie médicament de marque ou médicament générique.
Les MFE désigneraient surtout les produits de marque, alors que les MPF renverraient à toutes les molécules qui sont offertes sous une multitude de marques de commerce, que ce soit des produits de marque ou des produits génériques. Cela signifie qu’une fois que l’on offrira les copies génériques, le statut du produit de marque changera pour passer de MFE à MPF.
L’effet « MFE–MPF » serait différent de l’effet « substitution par un médicament générique » puisqu’il n’illustrerait que l’effet des médicaments passant du statut de « fournisseur exclusif » à celui de « plusieurs fournisseurs », ne reflétant ainsi que l’incidence initiale de la substitution par des médicaments génériques. De plus, l’effet « prix » sera également différent puisqu’il illustrera non seulement le véritable effet « prix », mais également les variations associées au passage d’un médicament de marque à un médicament générique dans une catégorie à plusieurs fournisseurs. Cela traduira les autres incidences de la substitution par des médicaments génériques.
Signalons qu’en fonction de l’augmentation ou de la réduction du nombre d’effets, il convient de modifier les formules des effets croisés, au besoin.
6. Limites
La méthodologie proposée de décomposition des dépenses en médicaments d’ordonnance comporte un certain nombre de limites, dont nous discuterons dans la présente section.
La méthodologie permet de décomposer les dépenses en médicaments d’ordonnance en fonction des facteurs de coût qu’il est possible d’extraire des bases de données administratives. Toutefois, en raison des limites que présentent les données disponibles, il est possible que certains facteurs importants n’aient pas été saisis (p. ex. la prévalence des maladies, les pratiques de prescription et les facteurs socioéconomiques).
Bien que les effets sont habituellement appelés facteurs, ce ne sont pas toujours des facteurs comme tels, mais plutôt des marqueurs pour des facteurs à proprement parler. L’effet « volume des ordonnances » et l’effet « médicament existant » en sont de bons exemples. Ils peuvent à leur tour être attribuables aux variations des taux d’incidence des maladies, aux pratiques de prescription des médecins, aux directives sur les traitements, aux politiques de remboursement, etc.
Étant donné que l’analyse des facteurs de coût fournit des résultats de haut niveau par rapport au marché analysé, elle est principalement utilisée pour signaler les secteurs de croissance. Cette information peut être utilisée pour mener des analyses plus approfondies des secteurs d’intérêt particuliers.
Les décompositions de coûts sont des analyses très complexes; c’est pourquoi il est nécessaire d’effectuer une assurance de la qualité et une validation afin d’assurer que l’on applique la méthodologie correctement. De plus, l’application de cette méthodologie exige une compréhension des avantages et des limites des données, une connaissance des aspects qui influencent la croissance spécifique des données analysées et une connaissance des champs d’application pertinents à la recherche.
La présente étude repose conceptuellement sur l’approche de décomposition de Laspeyres, qui est essentiellement une approche prospective. Il existe cependant plus d’une façon de mener les analyses de décomposition des coûts, y compris les décompositions idéales de Paasche et de Fisher. Ces indices de prix et de quantité ont leurs propres limites. Par conséquent, le choix de l’approche devrait dépendre du champ d’application de la recherche et de la façon dont seront utilisés les résultats.
7. Conclusion
Une analyse des facteurs de coût peut s’avérer un outil performant pour comprendre les pressions qui s’exercent sur le coût des médicaments et permettre aux décideurs et aux chercheurs d’analyser les tendances et de prévoir des résultats. De plus, la méthodologie peut être également employée dans le cadre d’analyses entre différentes administrations et de comparaisons entre pays, permettant ainsi de décomposer par sources les écarts quant aux ventes de médicaments ou aux dépenses dans ce domaine.
La présente étude permet de déterminer les principaux facteurs qui ont une incidence sur les dépenses en médicaments d’ordonnance et de proposer aux chercheurs les formules nécessaires à des analyses des facteurs de coût.
La méthodologie proposée peut faire l’objet d’ajustements et d’améliorations selon la disponibilité des données et selon la finalité d’une étude donnée et l’étendue de son analyse. En appliquant une méthodologie conventionnelle, il est possible d’effectuer des analyses des dépenses en ciblant spécifiquement certaines catégories thérapeutiques ou certains segments du marché. Par ailleurs, la méthodologie peut servir à des analyses entre différentes administrations afin de décomposer les sources des écarts quant aux dépenses par habitant.
Précisons que la méthodologie que propose le présent rapport porte sur une façon de mener une analyse des facteurs de coût; il en existe d’autres. Le procédé qui y est décrit a pour objet d’aider les chercheurs à assimiler les mécanismes de la méthodologie de décomposition des coûts et à établir leurs propres méthodologies en fonction de ce qu’ils visent à analyser.
8. Références
BERNDT, E.R., D.M. CUTLER, R.G. FRANK, Z. GRILICHES, J.P. NEWHOUSE et J.E. TRIPLETT. « Medical Care Prices and Output », Handbook of Health Economics, A. J. Culyer et J. P. Newhouse, éd., Amsterdam, Elsevier Science B. V., 2000.
CBO. Technological Change and the Growth of Health Care Spending, Washington, D.C., Congressional Budget Office, 2008 (consulté le 01-12-2013). Sur Internet : URL:http://www.cbo.gov/ftpdocs/89xx/doc8947/MainText.3.1.shtml.
CEPMB. Tendances des dépenses en médicaments – Programme des services de santé non assurés (volet pharmaceutique), 1999-2000 à 2001-2002, Ottawa, Conseil d’examen du prix des médicaments brevetés, 2004.
CEPMB. Rapport sommaire sur les tendances des prix des médicaments – Alberta, Saskatchewan, Manitoba, Ontario, Nouveau-Brunswick, Nouvelle-Écosse et Direction générale de la santé des Premières nations et des Inuits de Santé Canada. Pour la période de 1997-1998 à 2003-2004, Ottawa, Conseil d’examen du prix des médicaments brevetés, 2006.
CEPMB. Application de la dose quotidienne définie par l’Organisation mondiale de la santé dans les analyses de l’utilisation et des coûts des médicaments au Canada, Ottawa, Conseil d’examen du prix des médicaments brevetés, 2010 (consulté le 01-12-2013). Sur Internet : URL:http://www.pmprb-cepmb.gc.ca/CMFiles/Publications/Analytical%20Studies/NPDUIS-WHO-DDD-f.pdf.
CEPMB. Analyse des facteurs de coût associés aux frais d’exécution d’ordonnance assumés par les régimes publics d’assurance-médicaments, de 2001-2002 à 2007-2008, Ottawa, Conseil d’examen du prix des médicaments brevetés, 2011 (consulté le 01-12-2013). Sur Internet : URL:http://www.pmprb-cepmb.gc.ca/CMFiles/Publications/Analytical%20Studies/NPDUIS-DispensingFees-f-sept30.pdf.
DIEWERT, W.E. The Consumer Price Index and the Index Number Theory: A Survey, 2001. Vancouver : Vancouver School of Economics, The University of British Columbia, Discussion Paper 01-02.
DIVISION DE LA STATISTIQUE DES NATIONS UNIES. Updated System of National Accounts (SNA): Chapter 15: Price and volume measures, New York, Organisation des Nations Unies, 2008 (consulté le 01-12-2013). Sur Internet : URL:http://unstats.un.org/unsd/statcom/doc08/SNA-Chapter15.pdf.
GERDTHAM, U.G. et D. LUNDIN. « Why did drug spending increase during the 1990s? », PharmacoEconomics, vol. 22, no 1 (2004), p. 29-42.
ICIS. Facteurs d’accroissement des dépenses de santé : les faits, Ottawa, Institut canadien d’information sur la santé, 2011 (consulté le 01-12-2013). Sur Internet : URL:https://secure.cihi.ca/free_products/health_care_cost_drivers_the_facts_fr.pdf.
ICIS. Dépenses en médicaments au Canada, de 1985 à 2012, Ottawa, Institut canadien d’information sur la santé, 2013. Sur Internet : URL:https://secure.cihi.ca/free_products/Drug_Expenditure_2013_FR.pdf.
ICIS. Facteurs d’accroissement des dépenses en médicaments prescrits au Canada, Ottawa, Institut canadien d’information sur la santé, 2012 (consulté le 01-12-2013). Sur Internet : URL:http://www.cihi.ca/CIHI-ext-portal/pdf/internet/DRUG_SPEND_DRIVERS_FR.
MORGAN, S.G. « Quantifying Components of Drug Expenditure Inflation: The British Columbia Seniors’ Drug Benefit Plan », Health Services Research, vol. 37, no 5, (2002), p. 1243-1266.
MORGAN, S.G. « Drug Spending in Canada: Recent Trends and Causes », Medical Care, vol. 42, no 7 (2004), p. 635-642.
MORGAN, S.G. « Drug Expenditure Trends in the Canadian Provinces: Magnitude and Causes from 1998 to 2004 », Healthcare Policy, vol. 1, no 1 (2005), p. 85-99 (consulté le 01-12-2013). Sur Internet : URL:http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2585243/.
Annexe 1 – La décomposition de Laspeyres
La décomposition de Laspeyres abordée à la section 3.2 décrit le cas simple d’un seul produit pour lequel la dépense est une fonction de deux facteurs : le prix et la quantité. Une analyse des facteurs de coût dans le monde réel porte habituellement sur plusieurs produits pour lesquels la dépense en médicaments est une fonction de multiples facteurs. Ce genre de cadre de travail est traité en détail dans la présente annexe.
L’approche de Laspeyres est une approche prospective. Il y aurait lieu de l’employer pour répondre à la question suivante :
« Quelle est la part des dépenses effectuées cette année qui est strictement attribuable à des prix plus élevés? »
Cette approche devrait s’employer lorsque l’effet du prix et l’effet de la quantité doivent tenir compte de la hausse réelle et globale du prix et de la quantité, respectivement. Dans ce cas-ci, on sera en présence d’un effet croisé résiduel, ce qui correspond à l’interaction entre l’effet du prix et l’effet de la quantité. Si l’on tente d’attribuer un effet croisé, l’effet du prix ne sera pas égal à la hausse du prix et, dans le même ordre d’idée, l’effet de la quantité ne sera pas égal à l’augmentation de la quantité.
Extension à plusieurs produits
Cette extension nous oblige maintenant à penser à P et à Q comme des listes de valeurs correspondantes, c’est-à-dire des vecteurs de prix et de quantités associés. Travailler avec des vecteurs complique le calcul, mais l’on se sert du même cadre de base : soulignons que l’analyse présentée dans les équations (1) à (6) est encore valide6.
Dans le cas où seuls le prix et la quantité sont pris en compte, un effet du prix (ou de la quantité) positif sous-entend que le prix (ou la quantité) doit avoir augmenté entre la période de référence et la période en cours. Lorsque plusieurs prix et quantités entrent en ligne de compte, les choses se compliquent. Dans ce cas, il est possible d’avoir un effet du prix (ou effet de la quantité) positif si certains prix (ou quantités), ou même la plupart d’entre eux, ont chuté entre la période de référence et la période en cours. Pour voir comment cela peut se produire, soulignons que l’effet du prix dans l’équation (6) peut s’écrire de la façon suivante :
(A1) MP = [P(1) – P(0)]Q(0)
Donc, l’équation (7) peut être réécrite ainsi7 :
(A2) MP = [w1D1 + w2 D2 … + wNDN]X(0)
où Di est la variation du prix du produit i exprimée en pourcentage de son prix au cours de la période de référence, et wi est la part de la dépense au cours de la période de référence pour le produit i. Si D1, D2… DN renferment des valeurs positives et négatives, il est impossible de déterminer si MP sera positif ou négatif sans effectuer la somme du deuxième membre de l’équation (8). Cependant, en général, MP aura tendance à être positif (négatif) si des hausses de prix coïncident avec des parts importantes (négligeables) de la dépense et si des baisses de prix coïncident avec des parts négligeables (importantes) de la dépense. Un résultat similaire vaut dans le cas de l’effet de la quantité.
Dans le cas de produits multiples, la valeur positive ou négative de l’effet croisé ne peut pas être déterminée sans effectuer les calculs, même si l’analyste connaît l’orientation de l’effet du prix et de l’effet de la quantité. L’effet croisé a la forme et les propriétés d’une corrélation statistique entre des changements de prix et des changements de quantités. Par conséquent, si d’importantes variations de prix coïncident avec des variations importantes de quantité dans le même sens (ou en sens opposé), alors l’effet croisé aura tendance à être important et positif (ou négatif). D’autre part, si d’importantes variations de prix et de quantités ne coïncident pas (par exemple, si des hausses importantes de prix se limitent à un seul sous-ensemble de produits et que d’importantes variations de quantités sont apportées à un sous-ensemble totalement distinct), alors l’effet croisé aura tendance à être négligeable, et ce, même dans le cas de données faisant état de plusieurs variations importantes de prix et de quantités.
L’extension à des facteurs multiples
Supposons que la variable X à prendre en considération est déterminée par un ensemble de facteurs N Z1, Z2 … ZN selon une relation fonctionnelle connue :
(A3) X = F(Z1, Z2 … ZN)
Cela implique que :
(A4.1) X(0) = F[Z1(0), Z2(0) … ZN(0)]
(A4.2) X(1) = F[Z1(1), Z2(1) … ZN(1)]
Notre objectif est d’établir une décomposition de Laspeyres qui tient compte de la variation des dépenses dans leur intégralité en attribuant des parts de cette variation aux facteurs N et à leurs diverses combinaisons. Par analogie avec l’équation (6), cette décomposition inclura les effets du premier ordre (« directs ») N, définis par :
(A5) M1 (i) = F[Z1(0) … Zi(1) … ZN(0)] – F[Z1(0) … Zi(0) … ZN(0)] i = 1 … N
Conformément à l’approche Laspeyres, chaque effet du premier ordre M1,i est obtenu comme la variation dans X qui se serait produit seulement si le facteur Zi a changé.
Les effets du deuxième ordre (« croisement double ») sont définis par :
(A6) M2(i, j) = F[Z1(0) … Zi(1) … Zj(1) … ZN(0)]
– F[Z1(0) … Zi(0) … Zj(0) … ZN(0)]
– [M1(i) + M1(j)] i = 1 … N, j = 1 … N
Chaque effet du deuxième ordre est calculé comme la variation dans X qui se serait produit si les facteurs Zi et Zj avaient changé, après d’effet direct de chaque facteur. Soulignons qu’en supprimant les effets directs du deuxième membre de l’équation (A6), nous obtenons une expression qui représente fidèlement l’incidence des interactions entre les variations dans Zi et Zj sur la dépense. Cette expression comporte une composante de variation de la dépense qui est incrémentielle aux composantes attribuables aux effets directs de Zi et de Zj, ce qui signifie qu’elle peut être ajoutée aux effets directs sans les compter deux fois.
Pour produire un ensemble intégral des effets du deuxième ordre, l’équation (A6) doit être appliquée à chacun des couples distincts de facteurs que l’on peut imaginer. Le nombre de ces couples s’élèvera à N(N – 1)/2; par conséquent, il faudra procéder au calcul d’un même nombre d’effets du deuxième ordre8.
Les effets du troisième ordre (« croisement triple ») sont définis par l’équation :
(A7) M3(i, j, k) = F[Z1(0) … Zi(1) … Zj(1) … Zk(1) … ZN(0)]
– F[Z1(0) … Zi(0) … Zj(0) … Zk(0) … ZN(0)]
– [M2(i, j) + M2(i, k) + M2(j, k)]
– [M1(i) + M1(j) + M1(k)] i = 1 … N, j = 1 … N, k = 1 … N
C’est-à-dire que chaque effet du troisième ordre est calculé comme la variation dans X qui se serait produit si les facteurs Zi, Zj et Zk avaient changé, après avoir tenu compte de l’effet direct de chaque facteur et des trois effets du deuxième ordre de Zi, Zj et Zk. Pour produire un ensemble intégral d’effets du troisième ordre, l’équation (A6) doit être appliquée à chacun des trios distincts de facteurs qui soient. Le nombre de ces trios s’élèvera à N(N – 1)(N – 2)/6, d’où le nombre identique d’effets du troisième ordre.
Il est possible d’élaborer des ensembles d’un ordre supérieur d’une façon similaire à l’équation (13), jusqu’à ce que nous atteignions l’effet du Nième ordre :
(A8) MN (1, 2, … N) = F[Z1(1), Z2(1) … ZN(1)]
– F[Z1(0), Z2(0) … ZN(0)]
– yN - 1
où yN-1 représente la somme de tous les effets de tous les ordres de 1 jusqu’à (N – 1). En utilisant les équations (A4.1) et (A4.2) dans l’équation (A8), cela donne :
(A9) X(1) – X(0) = MN (1,2…N) + yN - 1
Le deuxième membre de l’équation (A9) comprend tous les effets de tous les ordres, c’est-à-dire tous les effets directs et croisés, calculés conformément à la procédure précitée. La somme de ces effets est égale à la variation dans X, tel que requis.
La méthode par décomposition décrite ci-dessus générera 2N – 1 effets distincts9. Cela implique que le nombre d’effets à calculer augmente de manière exponentielle avec le nombre des facteurs dont tient compte l’analyse, doublant (approximativement) avec chaque facteur supplémentaire. La majeure partie de cette augmentation s’explique par la prolifération d’effets croisés : ajouter un autre facteur à un ensemble préexistant de N génère un seul nouvel effet direct, mais 2N – 1 effets croisés de plus.
6 Il est important de bien comprendre que le deuxième membre de l’équation (6) générera toujours une seule valeur même si P et Q sont des vecteurs. Une forme spéciale de multiplication s’applique dans le cas des vecteurs. Supposons que A et B sont deux vecteurs qui renferment tous deux des valeurs V. Supposons par ailleurs que A = [a1, a2… aV] et que B = [b1, b2… bV]. Dans ce cas, le produit de A et B est défini comme la somme des produits de leurs valeurs de correspondance respectives, c’est-à-dire, AB = a1b1 + a2b2 …+ aVbV. Ce résultat est connu sous le nom de « produit scalaire » de A et B.
7 L’effet du prix dans l’équation (6) peut s’écrire sous forme de produit scalaire comme suit :
MP = Q1(0)[P1(1) – P1(0)] + Q2(0)[P2(1) – P2(0)]… + QV(0)[PV(1) – PV(0)]
En multipliant et en divisant chaque terme par le prix de la période de référence correspondante, cela nous permet d’écrire :
MP = P1(0)Q1(0) {[P1(1) – P1(0)]/P1(0)} + P2(0)Q2(0){[P2(1) – P2(0)]/P2(0)}…
+ PV(0)QV(0){[PV(1) – PV(0)]/PV(0)}
En multipliant et en divisant chaque terme par le prix de la période de référence, la dépense donne ceci :
MP = [P1(0)Q1(0)/X(0)] {[P1(1) – P1(0)]/P1(0)}X(0)
+ [P2(0)Q2(0)/X(0)]{[P2(1) – P2(0)]/P2(0)}X(0)…
+ [PV(0)QV(0)/X(0)]{[PV(1) – PV(0)]/PV(0)}X(0)
L’expression [Pi(0)Qi(0)/X(0)] est la part du produit i de la dépense au cours de la période de référence, alors que {[Pi(1) – Pi(0)]/Pi(0)} est la variation proportionnelle du prix du produit i.
8 Une formule bien connue génère le nombre des sous-ensembles distincts de l’élément Q distinct qui peuvent être formés à partir d’un ensemble plus grand d’éléments distincts N. Cette formule est C(Q,N) = N!/[Q!(N – Q)!], où I! = I(I – 1)(I – 2)… pour tout nombre entier relatif positif I. Si Q = 2, nous avons C(2,N) = N!/[2!(N – 2)!] = [N(N – 1)]/2.
9 Chaque Zi(t) peut prendre soit une valeur Zi(0), soit une valeur Zi(1). Cela signifie que le N-uplet [Z1(t), Z2(t)… ZN(t)] peut avoir 2N valeurs distinctes. Chacune de ces valeurs est associée à un effet direct distinct ou à un effet croisé distinct, sauf dans le cas de [Z1(0), Z2(0)… ZN(0)], qui définit la dépense au cours de la période de référence. Il y a donc 2N – 1 effets distincts à calculer au moment d’exécuter la décomposition généralisée de Laspeyres.
Annexe 2 – La décomposition de Paasche
L’approche de Laspeyres porte sur l’évaluation des incidences des variations des facteurs par rapport aux valeurs de tous les autres facteurs au cours d’une période de référence. En revanche, l’approche de Paasche porte sur l’évaluation de l’incidence de chaque facteur sur la dépense en médicaments en maintenant tous les autres facteurs à leurs valeurs pendant la période en cours.
Par conséquent, l’approche de Paasche est une approche rétrospective. Il faudrait l’employer pour répondre à la question qui suit :
« Jusqu’à quel point la dépense aurait-elle été moindre cette année aux prix de l’année dernière? »
En raison de sa nature hypothétique, il est peu probable que l’on fasse appel uniquement à cette approche comme instrument d’une analyse des facteurs de coût. Toutefois, il est possible de l’appliquer en conjugaison avec l’approche de Laspeyres à la décomposition idéale de Fisher.
Penchons-nous encore une fois sur le cas élémentaire « P fois Q ». La décomposition de Paasche débute par l’observation selon laquelle
(A10.1) P(0) = P(1) – [P(1) – P(0)]
(A10.2) Q(0) = Q(1) – [Q(1) – Q(0)]
En substituant les équations (10.1) et (10.2) dans l’équation (1), cela donne
(A11) X(1) – X(0) = P(0)Q(0) – {P(1) – [P(1) – P(0)]}{Q(1) – [Q(1) – Q(0)]}
Le deuxième membre de l’équation (11) se simplifie à :
(A12) X(1) – X(0) = [P(1) – P(0)]Q(1) + P(1)[Q(1) – Q(0)] – [P(1) – P(0)][Q(1) – Q(0)]
Les trois termes du deuxième membre de l’équation (A12) constituent le type Paasche de décomposition de la variation de la dépense :
Le premier terme du deuxième membre de l’équation (A12) est un indice des prix de Paasche, exprimé sous la forme d’une différence plutôt que d’un ratio. Il indique une mesure de l’incidence des variations de prix sur la dépense, évaluée en fonction des quantités durant la période en cours.
Le deuxième terme est un indice des quantités de Paasche, exprimé sous la forme d’une différence plutôt que d’un ratio. Il indique une mesure de l’incidence des variations de quantités sur la dépense, évaluée en fonction des prix durant la période en cours.
Le troisième terme correspond à l’effet croisé de Paasche. Il indique une mesure de l’incidence des interactions entre les variations de prix et les variations de quantités.
Une comparaison de l’équation (6) et de l’équation (A12) permet de révéler que l’effet croisé de Paasche est l’inversion logique de l’effet croisé de Laspeyres. Comme l’approche de Paasche porte sur une évaluation des effets directs des prix et des quantités aux valeurs durant la période en cours, chacun de ces effets comprend déjà l’incidence des interactions entre les variations des prix et des quantités. Dans ce cas-ci, il faut une correction pour éviter une double comptabilisation de l’incidence des interactions entre prix et quantités. L’effet croisé de Paasche effectue cette correction.
Annexe 3 – La décomposition idéale de Fisher
Les effets des prix et des quantités selon Laspeyres et selon Paasche sont aussi valides les uns que les autres, mais ils répondent à des questions différentes, puisque les uns sont déterminés dans le cadre d’une analyse prospective alors que les autres le sont à la suite d’une analyse rétrospective. Par conséquent, il en résulterait des estimations différentes des facteurs. Par ailleurs, en raison de la présence d’effets croisés, aucune de ces deux approches ne permet d’expliquer totalement la croissance des dépenses parmi les effets pris isolément.
Le recours aux moyennes symétriques a été proposé en vue de traiter de la question des limites des indices de Laspeyres et de Paasche. Ces moyennes symétriques peuvent être la moyenne arithmétique ou la moyenne géométrique des indices de Laspeyres et de Paasche, que l’on appelle « indice idéal de Fisher » (Diewert, 2001). L’approche de Fisher a été appliquée notamment dans d’autres études sur les facteurs de coût qui ont été publiées (Morgan, 2002, 2004, 2005). L’indice des prix idéal de Fisher est considéré comme étant la moyenne la « plus uniformément » pondérée des deux indices de prix, car il s’agit d’une moyenne symétrique et homogène et qu’elle satisfait à la condition de réversibilité dans le temps (Diewert, 2001).
L’approche idéale de Fisher est l’attribution intégrale de l’approche axée sur les dépenses. C’est une approche hybride à mi-chemin entre l’approche de Laspeyres et celle de Paasche en ce qu’elle associe les approches prospective et rétrospective et donne lieu à une attribution intégrale des effets croisés de chacun des effets pris isolément. Le même résultat pourrait être obtenu en distribuant en parts égales les effets croisés de Laspeyres en fonction de chacun des facteurs contribuant à la variation.
Il y a lieu d’appliquer l’approche idéale de Fisher lorsque l’analyse commande que les dépenses soient totalement attribuées aux effets pris isolément, en reconnaissant par ailleurs que chacun des effets prend part aux interactions avec tous les autres effets. Précisions que cette approche ne devrait être employée que lorsqu’une distribution à parts égales des effets croisés est jugée appropriée.
Le principe de l’indice idéal de Fisher est transférable à l’approche proposée dans le présent document, notamment en prélevant un échantillon de la moyenne des deuxièmes membres de l’équation des effets de Laspeyres (6) et de l’équation des effets Paasche (A12) plus haut dans le texte. Puisque ces deux expressions égalent la variation de la dépense, nous obtenons
(A13) X(1) – X(0) = [P(1) – P(0)][(1/2)Q(1) + (1/2)Q(0)]
+ [(1/2)P(1) + (1/2)P(0)][Q(1) – Q(0)]
Le deuxième membre de l’équation (A13) représente l’approche idéale de Fisher à la décomposition pour le cas à deux facteurs. Le premier terme du deuxième membre de l’équation (A13) est l’effet du prix, qui représente la mesure de l’incidence des variations de prix sur les dépenses, évaluée au point médian des quantités de la période de référence et de celles de la période en cours. Le deuxième terme est l’effet de la quantité, qui représente la mesure de l’incidence des variations de la quantité sur la dépense, évaluée au point médian des prix de la période de référence et de celles de la période en cours.
Soulignons que l’équation (A13) ne comporte pas un terme croisé. Pour en comprendre le motif, prenons note que
(A14.1) (1/2)P(1) + (1/2)P(0) = P(0) + (1/2)[P(1) – P(0)]
(A14.2) (1/2)Q(1) + (1/2)Q(0) = Q(0) + (1/2)[Q(1) – Q(0)]
En substituant les équations (A14.1) et (A14.2) dans (A15), cela donne
(A15) X(1) – X(0) = {[P(1) – P(0)][Q(0) + (1/2)[P(1) – P(0)][Q(1) – Q(0)]}
+ {[P(0)[Q(1) – Q(0)] + (1/2)[P(1) – P(0)][Q(1) – Q(0)]}
Les deux termes entre accolades du deuxième membre de l’équation (A15) correspondent à l’effet du prix et à l’effet de la quantité, respectivement. La comparaison de ceux-ci avec le prix, la quantité et les effets croisés de Laspeyres dans l’équation (6) permet de révéler que l’approche idéale de Fisher obtient ses effets du prix et ses effets de la quantité en ajoutant la moitié de l’effet croisé de Laspeyres à chacun des effets du prix et ses effets de la quantité de Laspeyres. De la même manière, l’approche idéale de Fisher peut diviser l’effet croisé de Paasche équitablement entre les effets du prix et les effets de la quantité de Paasche. Dans le présent document, cette approche porte le nom de « décomposition idéale de Fisher ».
Annexe 4 – Attribution intégrale des effets croisés
Étant donné les limites discutées à la section 3.3 au sujet de l’attribution intégrale des effets croisés, la recommandation consiste à signaler les effets croisés comme un tout distinct. Dans ce cas, les effets pris isolément seront signalés, comme l’indique la section 4, et la portion de la dépense qui résulte d’effets croisés sera signalée séparément.
Cependant, si l’attribution intégrale des effets croisés est souhaitée, il est possible de la réaliser en implémentant l’algorithme décrit dans la présente annexe, lequel présente le cadre permettant de distribuer également les effets croisés des effets pris isolément. Cette approche est semblable à la décomposition idéale de Fisher.
Prenons l’exemple du modèle à trois facteurs suivant : la dépense comme le produit du prix, de la quantité par requérant et de la population de requérants. Dans ce cas, il y aura quatre effets croisés de Laspeyres à calculer : trois doubles effets mettant en jeu des variations de deux des trois facteurs, ainsi qu’un effet triple où tous les trois facteurs entrent en jeu.
L’approche de décomposition idéale de Fisher requiert que chacun des doubles effets soit divisé également entre les deux facteurs contribuant à la variation. De même, le triple effet devrait être divisé également entre tous les trois facteurs contribuant à la variation. Exprimé sous forme algébrique, l’effet du prix idéal IP de Fisher dans ce cas-ci pourrait s’écrire ainsi :
(A16) IP = [P(1) – P(0)]Q(0)Z(0)
+ 1/2[P(1) – P(0)][Q(1) – Q(0)]Z(0)
+ 1/2[P(1) – P(0)]Q(0)[Z(1) – Z(0)]
+ 1/3[P(1) – P(0)][Q(1) – Q(0)][Z(1) – Z(0)]
où Z représente le nombre de requérants et Q devrait maintenant être interprété comme la quantité par requérant. Les expressions représentant Z et Q des effets idéaux de Fisher seraient construites d’une façon comparable à l’équation (A16). En ajoutant ces expressions à l’équation (A16), il est évident que les trois effets idéaux de Fisher tiennent compte de tous les sept effets directs et croisés de Laspeyres.
Bien que ce soit plus complexe, il est possible de produire une décomposition idéale de Fisher où il y a quatre facteurs ou plus à considérer. La clé consiste à appliquer uniformément le principe de la division en parts égales : lorsqu’un effet croisé implique des variations des facteurs Q, chacun des facteurs devrait se voir attribuer une part égale de cet effet croisé. Un algorithme pour ce procédé se lirait ainsi :
Étape 1. Calculer tous les effets croisés en appliquant l’approche généralisée de Laspeyres décrite ci-dessus.
Étape 2. Examiner chaque effet croisé double. Attribuer la moitié de chaque valeur aux deux facteurs contribuant à la variation.
Étape 3. Examiner chaque effet croisé triple. Attribuer le tiers de chaque valeur aux trois facteurs contribuant à la variation.
Étape 4. Continuer avec les étapes 2 et 3 pour chacun des effets croisés qui restent, attribuant des parts égales à l’effet de chacun des facteurs contribuant à la variation. Ce procédé prendra fin lorsqu’un Nième de l’effet croisé du Nième ordre pris isolément sera attribué à chacun des facteurs pris en compte dans le cadre de l’analyse.
Étape 5. Prendre la somme des effets directs de chaque facteur et les parts de tous les effets croisés attribués de l’étape 2 à l’étape 4. Cela produira une décomposition complète de la variation de la dépense en N éléments, chacun de ceux-ci étant associé de façon particulière à l’un des N facteurs pris en compte dans le cadre de l’analyse.
Annexe 5 – Effets croisés liés à la dépense en médicaments d’ordonnance
Comme nous l’avons indiqué, la méthodologie axée sur la décomposition des facteurs départage la variation de la dépense globale en une multitude d’effets directs et croisés. Le nombre des effets sera tributaire du nombre des facteurs pris en compte dans le cadre de l’analyse. S’il y a N facteurs, il y aura en tout 2N – 1 effets distincts, desquels N correspondra au nombre des effets directs et 2N – (N + 1) correspondra au nombre des effets croisés. Il est possible de déterminer les niveaux N – 1 des effets croisés, mettant en jeu les interactions de deux facteurs, de trois facteurs et ainsi de suite. Le nombre des effets croisés distincts de niveau Q correspondra au nombre des combinaisons distinctes de Q éléments qui peuvent être formés à partir de l’ensemble de N éléments à l’origine : cela se traduit par la formule bien connue C(N, Q) = N!/[Q!(N – Q)!)], où X! = X(X – 1)(X – 2)… 1.
Prenons l’exemple d’une décomposition qui permet d’attribuer une variation de la dépense à trois facteurs. Puisque N = 3 dans ce cas-ci, il y aura en tout 23 – 1 = 7 effets, desquels 3 seront des effets directs et 23 – (3 + 1) = 4 seront des effets croisés. Il y aura N – 1 = 2 niveaux d’effets croisés – niveau 2 (« effets croisés doubles ») mettant en jeu des interactions entre deux facteurs et niveau 3 (« effets croisés triples ») mettant en jeu l’interaction de tous les trois facteurs. Plus précisément, il y aura C(3,2) = 3 effets croisés de niveau 2 et C(3,3) = 1 effet croisé de niveau 3.
Soulignons que le nombre des effets distincts augmente de manière exponentielle en fonction du nombre des facteurs dans la décomposition, doublant (approximativement) avec l’ajout de chaque nouveau facteur. Cette augmentation s’explique principalement par la prolifération d’effets croisés : ajouter un autre facteur à un ensemble préexistant de N génère seulement un nouvel effet direct, mais 2N – 1 effets croisés de plus.
Si la formule 1 porte sur la décomposition de huit effets, elle repose en fait sur sept facteurs. Cela s’explique par le fait que les effets « médicament retiré du formulaire » et « nouveau médicament » dans la formule 1 peuvent également être considérés comme un seul et même effet « médicament retiré du formulaire et nouveau médicament ».
Par conséquent, les effets croisés du médicament sont composés de 120 effets combinés, comme décrits ci-dessous. Ajoutons qu’en modifiant la méthodologie de décomposition du coût afin de tenir compte d’un nombre supérieur ou inférieur de facteurs, il faut aussi revoir le nombre des effets croisés.
21 effets croisés doubles : 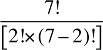 , soit :
, soit :
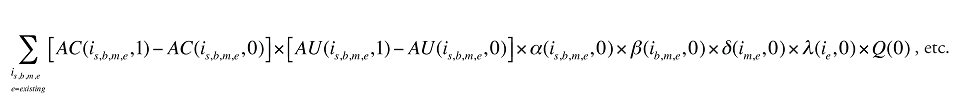
35 effets croisés triples : 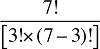 , soit :
, soit :

35 effets croisés quadruples : 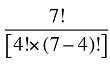 , soit :
, soit :
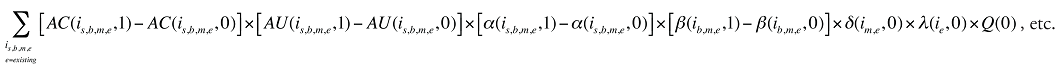
21 effets croisés quintuples : 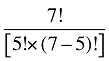 , soit :
, soit :

7 effets croisés sextuples : 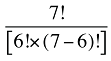 , soit :
, soit :
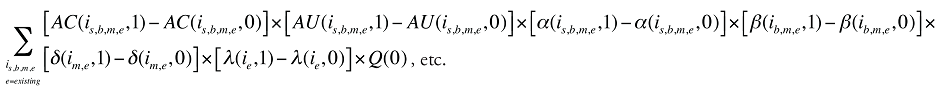
1 effet croisé septuple : 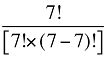 , à savoir :
, à savoir :
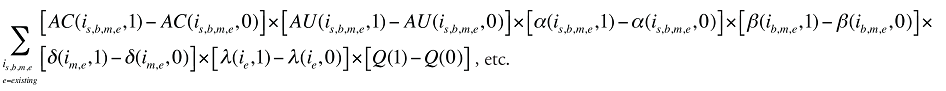
Annexe 6 – Effets croisés des facteurs démographiques
Les effets croisés des facteurs démographiques pour l’élément Coût des médicaments des dépenses pour les médicaments prescrits sont composés de quatre effets combinés, comme l’indiquent en détail les formules que voici.
3 effets croisés doubles : 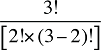
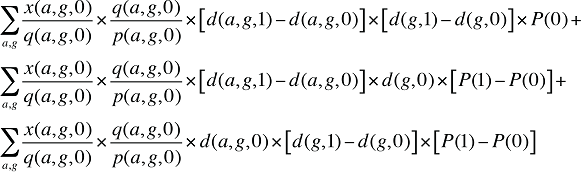
1 effet croisé triple : 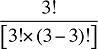
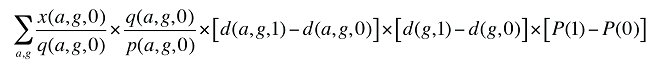
D’une manière semblable, les effets croisés des facteurs démographiques dans le cas de l’élément « Frais d’exécution des ordonnances des dépenses pour les médicaments prescrits » peuvent être déterminés en remplaçant le coût du médicament x(a,g,t) dans les formules ci-dessus par les frais d’exécution des ordonnances f(a,g,t).
Annexe 7 – Effets croisés des frais d’exécution des ordonnances
Les effets croisés des frais d’exécution des ordonnances sont composés de quatre effets combinés tel qu’indiqué en détail dans les formules que voici.
3 effets croisés doubles : 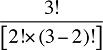
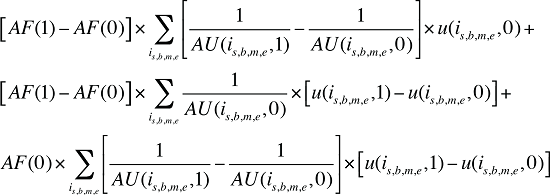
1 effet croisé triple : 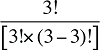
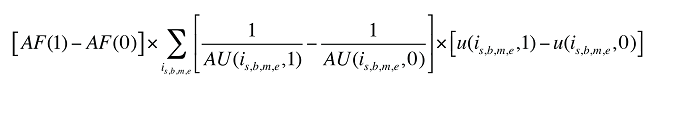
Annexe 8 : Effets croisés du montant versé par le bénéficiaire
Les effets croisés du montant versé par le bénéficiaire sont détaillés ci-dessous.
10 effets croisés doubles : 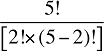 , soit :
, soit :
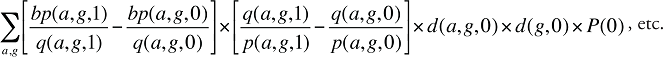
10 effets croisés triples : 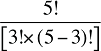 , soit :
, soit :
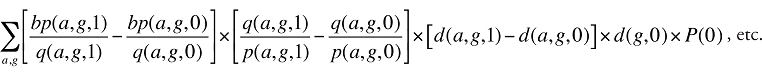
5 effets croisés quadruples : 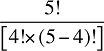 , soit :
, soit :

1 effet croisé quintuple : 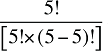 , soit :
, soit :
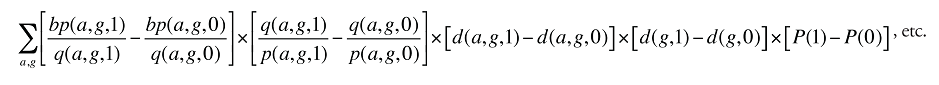
Annexe 9 – Exemple simplifié d’une analyse des facteurs de coût: les effets « médicament existant », « médicament retiré du formulaire » et « nouveau médicament »
La présente annexe offre un exemple simplifié de la façon de décomposer le coût des médicaments, ou les ventes de médicaments, en mettant en relief les effets « médicament existant », « médicament retiré du formulaire » et « nouveau médicament » dont il était question à la section 4.1.
Prenons l’exemple de quatre molécules – A, B, C et D – avec différents types de médicaments, prix, quantités et les ventes et les coûts correspondants, comme l’indique le tableau A9.1.
Tableau A9.1. Exemple hypothétique d’un marché composé de quatre produits : le prix multiplié par la quantité
table>blank
Type de médicament
Molécule active
Prix
Quantité
Total des coûts (ventes)
ie
im
p(im,e,0)
p(im,e,1)
q(im,e,0)
q(im,e,1)
x(im,e,0)
x(im,e,1)
Nouveau
A
20 $
–
33
–
660 $
Existant
B
10 $
12 $
40
33
400 $
396 $
Existant
C
15 $
17 $
50
44
750 $
748 $
Retiré du formulaire
D
5 $
10
–
50 $
–
Total
Q(0) = 100
Q(1) = 110
X(0) = 1 200 $
X(1) = 1 804 $
Dquantité = 10 (10 %)
Dcoût = 604 $ (50,3 %)
La dépense au cours d’une période donnée peut s’écrire comme ceci :
(A17)
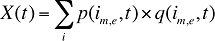
où :
im,e est le produit d’une molécule (m) précise et un statut (e) du médicament existant-retiré du formulaire-nouveau
t est une constante correspondant à l’une des deux périodes visées par l’analyse
X(t) est le montant total de la dépense en médicaments ou des ventes de ces médicaments au cours de la période t
p(im,e,t) est le coût ou le prix moyen par unité physique du produit im,e au cours de la période t
q(im,e,t) est la part im,e du produit du volume total (exprimé en ordonnances) au cours de la période t
Notons que q(im,e,t) = w(im,e,t) X Q(t) puis, que l’équation (A17) se transforme ainsi :
(A18)
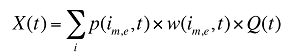
où :
w(im,e,t) est la part im,e du produit du volume total (exprimé en ordonnances) au cours de la période t
Q(t) est le volume total des ordonnances au cours de la période t
Le tableau A9.1 peut s’écrire comme le tableau A9.2.
Tableau A9.2. Exemple hypothétique d'un marché composé de quatre produits : le recours aux parts de marché
blank
| Type de médicament |
Molécule |
Prix |
Parts |
Quantité totale |
Total des coûts (ventes) |
| ie |
im |
p(im,e,0) |
p(im,e,1) |
w(im,e,0) |
w(im,e,1) |
Q(0) |
Q(1) |
x(im,e,0) |
x(im,e,1) |
| Nouveau |
A |
|
20 $ |
– |
30 % |
100 |
110 |
– |
660 $ |
| Existant |
B |
10 $ |
12 $ |
40 % |
30 % |
100 |
110 |
400 $ |
396 $ |
| Existant |
C |
15 $ |
17 $ |
50 % |
40 % |
100 |
110 |
750 $ |
748 $ |
| Retiré du formulaire |
D |
5 $ |
|
10 % |
– |
100 |
110 |
50 $ |
– |
| |
Total |
|
100 % |
100 % |
|
X(0) = 1 200 $ |
X(1) = 1 804 $ |
|
Dcoût = 604 $
(50,3 %) |
Notons qu’il s’agit d’une version simplifiée de l’équation (7) à la section 4.1. L’équation (A17) repose sur l’hypothèse selon laquelle la quantité est exprimée en unités plutôt qu’en demandes de remboursement, et que les produits n’ont pas une combinaison (s) particulière de dosage-forme galénique, ou n’ont pas une indication (b) de médicament de marque ou médicament générique, ou que ces caractéristiques ne sont pas pertinentes.
Comme nous le mentionnions à la section 4.1, chaque part w(im,e,t) prise isolément peut être décomposée en plusieurs parts de la façon suivante :
où : 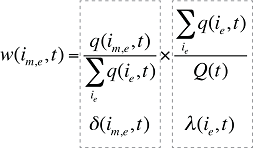
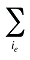 est la somme de la quantité de tous les produits i dont le statut (e) « médicament existant », « médicament retiré du formulaire » ou « nouveau médicament » est identique.
est la somme de la quantité de tous les produits i dont le statut (e) « médicament existant », « médicament retiré du formulaire » ou « nouveau médicament » est identique.
d(im,e,t) est la part de la somme des quantités de produits i avec la même molécule (m) et le même statut (e) « médicament existant », « médicament retiré du formulaire » ou « nouveau médicament » sur la somme des quantités de tous les produits dont le statut (e) « médicament existant », « médicament retiré du formulaire » ou « nouveau médicament » est identique.
l(ie,t) est la part de la somme des quantités de produits i dont le statut (e) « médicament existant », « médicament retiré du formulaire » ou « nouveau médicament » est identique sur la somme des quantités de tous les produits au cours de la période visée.
L’équation (A18) peut être reformulée de la façon suivante : 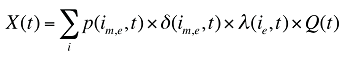
Comme dans le cas de la formule 1, l’effet « médicament existant », « médicament retiré du formulaire » ou « nouveau médicament » peut se décomposer comme suit :

où :
 est la somme de tous les médicaments « existants » et « retirés du formulaire », et
est la somme de tous les médicaments « existants » et « retirés du formulaire », et
 est la somme de tous les médicaments « existants » et « nouveaux ».
est la somme de tous les médicaments « existants » et « nouveaux ».
Dans l’exemple présenté au tableau A9.1 et au tableau A9.2, il est possible de décomposer encore davantage les parts des produits en fonction des types « médicament existant », « médicament retiré du formulaire » et « nouveau médicament », comme l’illustre le tableau A9.3.
Tableau A9.3. Exemple hypothétique d'un marché composé de quatre produits : le recours élargi aux parts de marché
blank
| Type de médicament |
Molécule |
Prix |
Parts de
 |
Parts de
 |
Parts de

|
Quantité totale |
Total des coûts
(vente) |
| ie |
im |
P(0) |
P(1) |
d(im,e,0) |
d(im,e,1) |
l(ie,0) |
l(ie,1) |
l(ie,0) |
l(ie,1) |
Q(0) |
Q(1) |
x(im,e,0) |
x(im,e,1) |
| Nouveau |
A |
|
20 $ |
|
100 % |
|
|
|
30 % |
100 |
110 |
– |
660 $ |
| Existant |
B |
10 $ |
12 $ |
44 % |
43 % |
90 % |
100 % |
100 % |
70 % |
100 |
110 |
400 $ |
396 $ |
| Existant |
C |
15 $ |
17 $ |
56 % |
57 % |
90 % |
100 % |
100 % |
70 % |
100 |
110 |
750 $ |
748 $ |
| Retiré du formulaire |
D |
5 $ |
|
100 % |
|
10 % |
|
|
|
100 |
110 |
50 $ |
– |
| |
Total |
|
X(0)=
1 200 $ |
X(1)=
1 804 $ |
|
Dcoût = 604 $ (50,3 %) |
Soulignons que l'effet « médicament retiré du formulaire » se limite aux médicaments « existants » et « retirés du formulaire ». 
Le terme l(i,1) prend la valeur 1 dans le cas des médicaments existants et 0 dans celui des médicaments « retirés du formulaire », car il n’y a aucun médicament « retiré du formulaire » au cours de la période 1.
Soulignons aussi que l’effet « nouveau médicament » se limite à la des « médicaments existants » et des « nouveaux médicaments ».
Le terme l(i,0) prend la valeur 1 dans le cas de médicaments existants et 0 dans celui des nouveaux médicaments au cours de la période 0.
En guise d’étape de validation, les valeurs pour le total des ventes ou des coûts surlignés en orange dans les tableaux A9.1 à A9.3 devraient rester inchangées tout au long du processus de décomposition.
Les valeurs du tableau A9.3 peuvent servir à calculer aisément l’équation (A19). Les résultats sont présentés au tableau A9.4.
Tableau A9.4. Effets individuels de l’analyse des facteurs de coût
blank
Type de médicament
ie |
Molécule im |
Effet du prix |
Effet « médicament existant » |
Effet « médicament retiré du formulaire » |
Effet « nouveau médicament » |
Effet de
la quantité |
| Nouveau |
A |
– |
– |
– |
600 $ |
– |
| Existant |
B |
80 $ |
-16 $ |
44 $ |
-129 $ |
40 $ |
| Existant |
C |
100 $ |
24 $ |
83 $ |
-257 $ |
75 $ |
| Retiré du formulaire |
D |
– |
– |
-50 $ |
– |
5 $ |
| |
Total
(% de Dcoût) |
180 $ (15,0 %) |
8 $ (0,7 %) |
78 $ (6,5 %) |
214 $ (17,9 %) |
120 $ (10,0 %) |
| |
Total |
|
600 $ (50,0 %) |
|
Également comme étape de validation, le résultat de l’effet de la quantité exprimé en pourcentage de Dcoût de 10 % devrait être identique à la variation de la quantité de médicaments au cours des deux périodes, comme l’indique le tableau A9.1.
La différence entre la somme de tous les effets au tableau A9.4 estimée à 600 $ (ou 50,0 % de X(0)) et la différence entre les ventes, ou coûts, des deux périodes estimées à 604 $ (ou 50,0 % de X(0)) comme l’indiquent les tableaux A9.1 à A9.3 s’expliquent par les effets croisés qui figurent en détail dans l’équation (A20) ci-dessous. Par souci de simplicité, on les calcule à l’aide de l’équation (A18).
(A20)

Les formules pour les effets croisés qui sont appliquées à l’exemple donnent les résultats suivants.
Tableau A9.5. Effets croisés de l’analyse des facteurs de coût
blank
Type de médicament
ie |
Molécule
im |
Effet croisé 1 |
Effet croisé 2 |
Effet croisé 3 |
Effet croisé 4 |
Total |
| Nouveau |
A |
– |
– |
60 $ |
– |
60 $ |
| Existant |
B |
-20 $ |
8 $ |
-10 $ |
-2 $ |
-24 $ |
| Existant |
C |
-20 $ |
10 $ |
-15 $ |
-2 $ |
-27 $ |
| Retiré du formulaire |
D |
– |
– |
-$5 |
– |
-5 $ |
| |
-40 $ |
18 $ |
$30 |
-4 $ |
|
| |
Total (% de D coût) |
|
4,00 $ (0,3 %) |
Soulignons que la somme des effets croisés au tableau A9.4 est de 4 $ (0,3 % de X(0)). Additionnée au total des effets pris isolément au tableau A9.5, soit 600 $ (ou 50,0 % de X(0)), cela donne le montant exact des ventes, ou coûts, différentiels entre les deux périodes de 604 $ (ou 50,3 % de X(0)), tel que calculé aux tableaux A9.1 à A9.3.
L’exemple dans la présente section offre une explication simple de l’analyse des facteurs de coût. La même idée peut s’appliquer à des ensembles de données plus grands et à des effets plus nombreux, comme le mentionne le rapport à proprement parler.
Cet exemple permet également d’expliquer la façon de distribuer les effets croisés lorsqu’on souhaite effectuer une attribution intégrale des coûts de chacun des effets.
Par exemple, l’effet croisé 2 de 18 $ au tableau A9.5 serait subdivisé en deux parties. La moitié serait attribuée à l’effet du prix et l’autre à l’effet de la quantité dans le tableau A9.4. En appliquant la même logique, on subdiviserait en trois l’effet croisé triple, attribuant le tiers à l’effet du prix, à l’effet « médicament existant » et à l’effet de la quantité au tableau A9.4.
Mentionnons que, dans ce cas-ci, l’effet de la quantité tiendra compte non seulement de l’augmentation de 10 % de la quantité, mais également de l’interaction avec les autres facteurs : bien que la quantité ait augmenté, l’augmentation s’explique aussi par l’arrivée de nouveaux médicaments, plus chers, ainsi que par des hausses du prix de médicaments existants.